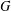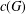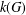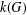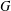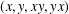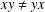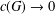Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Martin-Pizarro, Amador
and
Palacín, Daniel
2024.
Complete type amalgamation for nonstandard finite groups.
Model Theory,
Vol. 3,
Issue. 1,
p.
1.
KOUSEK, IOANNIS
2025.
Revisiting sums and products in countable and finite fields.
Ergodic Theory and Dynamical Systems,
p.
1.