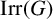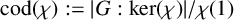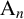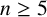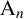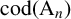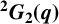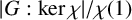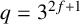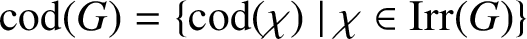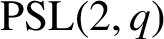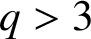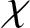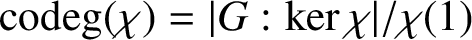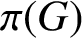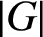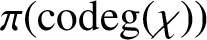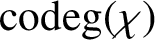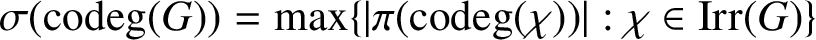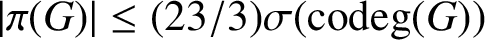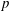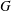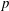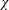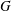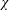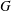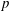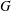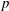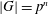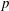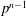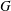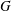Refine search
Actions for selected content:
7 results
 $M_{p}$-GROUPS AND BRAUER CHARACTER DEGREES
$M_{p}$-GROUPS AND BRAUER CHARACTER DEGREES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 09 May 2025, pp. 1-5
-
- Article
- Export citation
ON THE CHARACTERISATION OF ALTERNATING GROUPS BY CODEGREES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 26 January 2024, pp. 115-120
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RECOGNISING REE GROUPS
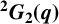 $\boldsymbol {{}^{2}G_{2}(q)}$ USING THE CODEGREE SET
$\boldsymbol {{}^{2}G_{2}(q)}$ USING THE CODEGREE SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 28 September 2022, pp. 125-132
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON A QUESTION OF MORETÓ
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 13 April 2022, pp. 306-309
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN ANALOGUE OF HUPPERT’S CONJECTURE FOR CHARACTER CODEGREES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 08 February 2021, pp. 278-286
- Print publication:
- October 2021
-
- Article
- Export citation
ON ANALOGUES OF HUPPERT’S CONJECTURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 18 January 2021, pp. 272-277
- Print publication:
- October 2021
-
- Article
- Export citation
Character Codegrees of Maximal Class
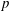 $p$-groups
$p$-groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 25 September 2019, pp. 328-334
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation