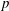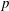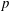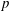Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Croome, Sarah
and
Lewis, Mark L.
2020.
𝑝-groups with exactly four codegrees.
Journal of Group Theory,
Vol. 23,
Issue. 6,
p.
1111.
Qian, Guohua
2021.
Element orders and character codegrees.
Bulletin of the London Mathematical Society,
Vol. 53,
Issue. 3,
p.
820.
Moretó, Alexander
2022.
Character degrees, character codegrees and nilpotence class of p-groups.
Communications in Algebra,
Vol. 50,
Issue. 2,
p.
803.
Wang, Zhongbi
Qian, Guohua
Lv, Heng
and
Chen, Guiyun
2024.
On the average codegree of a finite group.
Journal of Algebra and Its Applications,
Vol. 23,
Issue. 05,
Liu, Yang
and
Yang, Yong
2025.
Two results on character codegrees.
Journal of Algebra and Its Applications,
Vol. 24,
Issue. 06,
Prajapati, Sunil Kumar
and
Udeep, Ayush
2025.
On the relation of character codegrees and the minimal faithful quasi-permutation representation degree of
p
-groups
.
Communications in Algebra,
Vol. 53,
Issue. 1,
p.
450.