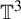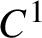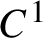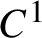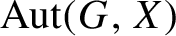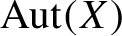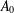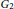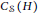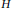Refine search
Actions for selected content:
10 results
Centralizers of derived-from-Anosov systems on
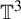 ${\mathbb T}^3$: rigidity versus triviality
${\mathbb T}^3$: rigidity versus triviality
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 02 August 2021, pp. 2841-2865
- Print publication:
- September 2022
-
- Article
- Export citation
Accessibility and centralizers for partially hyperbolic flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 835-854
- Print publication:
- March 2022
-
- Article
- Export citation
Minimal flows with arbitrary centralizer
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 29 December 2020, pp. 310-320
- Print publication:
- January 2022
-
- Article
- Export citation
ON GRADED SYMMETRIC CELLULAR ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 July 2019, pp. 349-362
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
The Universal Enveloping Algebra of the Schrödinger Algebra and its Prime Spectrum
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 4 / 01 December 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 688-703
- Print publication:
- 01 December 2018
-
- Article
-
- You have access
- Export citation
Order 3 Elements in G2 and Idempotents in Symmetric Composition Algebras
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 5 / 01 October 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1038-1075
- Print publication:
- 01 October 2018
-
- Article
-
- You have access
- Export citation
A WEAK HILBERT SPACE THAT IS A TWISTED HILBERT SPACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 15 May 2018, pp. 855-867
- Print publication:
- May 2020
-
- Article
- Export citation
Classification of Simple Weight Modules over the Schrödinger Algebra
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 1 / 01 March 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 16-39
- Print publication:
- 01 March 2018
-
- Article
-
- You have access
- Export citation
On the simplest centralizer of a language
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 40 / Issue 2 / April 2006
- Published online by Cambridge University Press:
- 20 July 2006, pp. 295-301
- Print publication:
- April 2006
-
- Article
- Export citation
On properties of group closures of one-to-one transformations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 2 / October 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 213-229
- Print publication:
- October 2005
-
- Article
-
- You have access
- Export citation