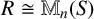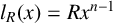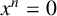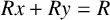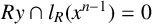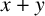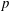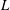Refine search
Actions for selected content:
4 results
GRAPH CHARACTERISATION OF THE ANNIHILATOR IDEALS OF LEAVITT PATH ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 15 February 2024, pp. 498-507
- Print publication:
- December 2024
-
- Article
- Export citation
A CHARACTERISATION OF MATRIX RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 08 August 2022, pp. 95-101
- Print publication:
- February 2023
-
- Article
- Export citation
Annihilators of the Ideal Class Group of a Cyclic Extension of an Imaginary Quadratic Field
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 1395-1419
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Relative $K_{0}$, annihilators, Fitting ideals and Stickelberger phenomena
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 90 / Issue 3 / May 2005
- Published online by Cambridge University Press:
- 22 April 2005, pp. 545-590
- Print publication:
- May 2005
-
- Article
- Export citation