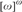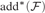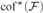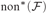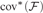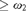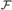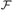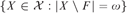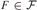Refine search
Actions for selected content:
2 results
MORE ON YET ANOTHER IDEAL VERSION OF THE BOUNDING NUMBER
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-16
-
- Article
- Export citation
TOWERS IN FILTERS, CARDINAL INVARIANTS, AND LUZIN TYPE FAMILIES
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 23 October 2018, pp. 1013-1062
- Print publication:
- September 2018
-
- Article
- Export citation