Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-28T23:57:58.406Z Has data issue: false hasContentIssue false
  • English
  • Français

MORE ON YET ANOTHER IDEAL VERSION OF THE BOUNDING NUMBER

Part of: Set theory

Published online by Cambridge University Press:  27 January 2025

ADAM KWELA Open the ORCID record for ADAM KWELA [Opens in a new window]
ADAM KWELA*
Affiliation:
INSTITUTE OF MATHEMATICS FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS, UNIVERSITY OF GDAŃSK UL. WITA STWOSZA 57 80-308 GDAŃSK POLAND Url: https://mat.ug.edu.pl/~akwela
*
E-mail: Adam.Kwela@ug.edu.pl
Get access Rights & Permissions [Opens in a new window]

Abstract

This is a continuation of the paper [J. Symb. Log. 87 (2022), 1065–1092]. For an ideal $\mathcal {I}$ on 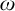$\omega $ we denote $\mathcal {D}_{\mathcal {I}}=\{f\in \omega ^{\omega }: f^{-1}[\{n\}]\in \mathcal {I} \text { for every } n\in \omega \}$ and write 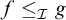$f\leq _{\mathcal {I}} g$ if 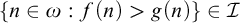$\{n\in \omega :f(n)>g(n)\}\in \mathcal {I}$, where 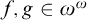$f,g\in \omega ^{\omega }$.

We study the cardinal numbers 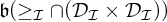$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}} \times \mathcal {D}_{\mathcal {I}}))$ describing the smallest sizes of subsets of 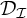$\mathcal {D}_{\mathcal {I}}$ that are unbounded from below with respect to 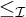$\leq _{\mathcal {I}}$.

In particular, we examine the relationships of 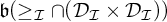$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}} \times \mathcal {D}_{\mathcal {I}}))$ with the dominating number 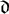$\mathfrak {d}$. We show that, consistently, 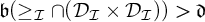$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}} \times \mathcal {D}_{\mathcal {I}}))>\mathfrak {d}$ for some ideal 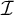$\mathcal {I}$, however 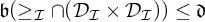$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}} \times \mathcal {D}_{\mathcal {I}}))\leq \mathfrak {d}$ for all analytic ideals 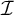$\mathcal {I}$. Moreover, we give example of a Borel ideal with 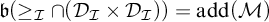$\mathfrak {b}(\geq _{\mathcal {I}}\cap (\mathcal {D}_{\mathcal {I}} \times \mathcal {D}_{\mathcal {I}}))=\operatorname {\mathrm {add}}(\mathcal {M})$.

Keywords

idealfilterBorel idealanalytic idealdominating numberideal with topological representationbounding numberquasi-normal convergencequasi-normal spaceQN-space

MSC classification

Primary: 03E05: Other combinatorial set theory
Secondary: 03E15: Descriptive set theory 03E17: Cardinal characteristics of the continuum 03E35: Consistency and independence results
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 16
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barbarski, P., Filipów, R., Mrożek, N., and Szuca, P., When does the Katětov order imply that one ideal extends the other? Colloquium Mathematicum , vol. 130 (2013), pp. 91–102.CrossRefGoogle Scholar
Bartoszyński, T., Invariants of measure and category , Handbook of Set Theory, vols. 1–3 (Matthew, F. and Akihiro, K., editors), Springer, Dordrecht, 2010, pp. 491–555.CrossRefGoogle Scholar
Bartoszyński, T. and Shelah, S., Closed measure zero sets . Annals of Pure and Applied Logic , vol. 58 (1992), no. 2, pp. 93–110.CrossRefGoogle Scholar
Blass, A., Combinatorial cardinal characteristics of the continuum , Handbook of Set Theory, vols. 1–3 (Matthew, F. and Akihiro, K., editors), Springer, Dordrecht, 2010, pp. 395–489.CrossRefGoogle Scholar
Bukovský, L., On $wQN_\ast$ and $wQN^\ast$ spaces. Topology and Its Applications , vol. 156 (2008), no. 1, pp. 24–27.CrossRefGoogle Scholar
Bukovský, L., The structure of the real line , Instytut Matematyczny Polskiej Akademii Nauk , Monografie Matematyczne (New Series) [Mathematics Institute of the Polish Academy of Sciences, Mathematical Monographs (New Series)], 71, Birkhäuser/Springer Basel AG, Basel, 2011.Google Scholar
Bukovský, L., Das, P., and Šupina, J., Ideal quasi-normal convergence and related notions . Colloquium Mathematicum , vol. 146 (2017), no. 2, pp. 265–281.CrossRefGoogle Scholar
Bukovský, L. and Haleš, J., QN-spaces, wQN-spaces and covering properties . Topology and Its Applications , vol. 154 (2007), no. 4, pp. 848–858.CrossRefGoogle Scholar
Bukovský, L., Recław, I., and Repický, M., Spaces not distinguishing pointwise and quasinormal convergence of real functions . Topology and Its Applications , vol. 41 (1991), no. 1–2, pp. 25–40.CrossRefGoogle Scholar
Bukovský, L., Recław, I., and Repický, M., Spaces not distinguishing convergences of real-valued functions . Topology and Its Applications , vol. 112 (2001), no. 1, pp. 13–40.CrossRefGoogle Scholar
Canjar, M., Countable ultraproducts without CH* . Annals of Pure and Applied Logic , vol. 37 (1988), no. 1, pp. 1–79.CrossRefGoogle Scholar
Canjar, R. M., Model-theoretic properties of countable ultraproducts without the continuum hypothesis, Ph.D. thesis, University of Michigan, ProQuest LLC, Ann Arbor, 1982.Google Scholar
Canjar, R. M., Cofinalities of countable ultraproducts: The existence theorem . Notre Dame Journal of Formal Logic , vol. 30 (1989), no. 4, pp. 539–542.CrossRefGoogle Scholar
Das, P. and Chandra, D., Spaces not distinguishing pointwise and $\mathcal {I}$ -quasinormal convergence . Commentationes Mathematicae Universitatis Carolinae , vol. 54 (2013), no. 1, pp. 83–96.Google Scholar
Debs, G. and Raymond, J. S., Filter descriptive classes of Borel functions . Fundamenta Mathematicae , vol. 204 (2009), no. 3, pp. 189–213.CrossRefGoogle Scholar
Farah, I. and Solecki, S., Two $F_{\sigma\delta}$   ideals . Proceedings of the American Mathematical Society , vol. 131 (2003), no. 6, pp. 1971–1975.CrossRefGoogle Scholar
Filipów, R. and Kwela, A., Yet another ideal version of the bounding number . The Journal of Symbolic Logic , vol. 87 (2022), no. 3, pp. 1065–1092.CrossRefGoogle Scholar
Filipów, R. and Staniszewski, M., Pointwise versus equal (quasi-normal) convergence via ideals . Journal of Mathematical , vol. 422 (2015), no. 2, pp. 995–1006.Google Scholar
Fremlin, D. H., Consequences of Martin’s Axiom , Cambridge Tracts in Mathematics, 84, Cambridge University Press, Cambridge, 1984.CrossRefGoogle Scholar
Hrušák, M., Combinatorics of filters and ideals , Set Theory and Its Applications , Contemporary Mathematics, 533, American Mathematical Society, Providence, 2011, pp. 29–69.CrossRefGoogle Scholar
Kankaanpää, T., Remarks on gaps in dense ( $\mathbb{Q}$ )/nwd. Mathematical Logic Quarterly , vol. 59 (2013), nos. 1–2, pp. 51–61.CrossRefGoogle Scholar
Katětov, M., Products of filters . Commentationes Mathematicae Universitatis Carolinae , vol. 9 (1968), pp. 173–189.Google Scholar
Katětov, M., On Descriptive Classes of Functions , Theory of Sets and Topology (in honour of Felix Hausdorff, 1868–1942), VEB Deutsch. Verlag Wissensch., Berlin, 1972, pp. 265–278.Google Scholar
Katětov, M., On descriptive classification of functions , General Topology and its Relations to Modern Analysis and Algebra, III (Proceedings of Third Prague Topological Symposium, 1971), (Novák, J., Frolik, Z. and Pták, V., editors), Academia, Prague, 1972, pp. 235–242.Google Scholar
Kunen, K., Set Theory , Studies in Logic (London), 34, College Publications, London, 2011.Google Scholar
Kwela, A., Ideal weak QN-spaces . Topology and Its Applications , vol. 240 (2018), pp. 98–115.CrossRefGoogle Scholar
Kwela, A. and Sabok, M., Topological representations. Journal of Mathematical Analysis and Applications , vol. 422 (2015), no. 2, pp. 1434–1446.CrossRefGoogle Scholar
Recław, I., Metric spaces not distinguishing pointwise and quasinormal convergence of real functions . Bulletin of the Polish Academy of Sciences. Mathematics , vol. 45 (1997), no. 3, pp. 287–289.Google Scholar
Repický, M., Spaces not distinguishing convergences . Commentationes Mathematicae Universitatis Carolinae , vol. 41 (2000), no. 4, pp. 829–842.Google Scholar
Repický, M., Spaces not distinguishing ideal convergences of real-valued functions . Real Analysis Exchange , vol. 46 (2021), no. 2, pp. 367–394.Google Scholar
Repický, M., Spaces not distinguishing ideal convergences of real-valued functions, II . Real Analysis Exchange , vol. 46 (2021), no. 2, pp. 395–421.Google Scholar
Sabok, M. and Zapletal, J., Forcing properties of ideals of closed sets . Journal of Symbolic Logic , vol. 76 (2010), pp. 4011–4039.Google Scholar
Sakai, M., The sequence selection properties of $C_p(X)$ . Topology and Its Applications , vol. 154 (2007), no. 3, pp. 552–560.CrossRefGoogle Scholar
Šottová, V. and Šupina, J., Principle ${\text{S}}_1(\mathcal{P},\mathcal{R})$ :  ideals and functions . Topology and Its Applications , vol. 258 (2019), pp. 282–304.CrossRefGoogle Scholar
Staniszewski, M., On ideal equal convergence II . Journal of Mathematical Analysis and Applications , vol. 451 (2017), no. 2, pp. 1179–1197.CrossRefGoogle Scholar
Šupina, J., Ideal QN-spaces . Journal of Mathematical Analysis and Applications , vol. 435 (2016), no. 1, pp. 477–491.CrossRefGoogle Scholar
Tsaban, B. and Zdomskyy, L., Hereditarily Hurewicz spaces and Arhangel’skiĭ sheaf amalgamations . Journal of the European Mathematical Society , vol. 14 (2012), no. 2, pp. 353–372.CrossRefGoogle Scholar