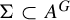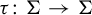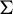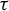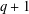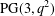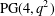Refine search
Actions for selected content:
4 results
Invariant sets and nilpotency of endomorphisms of algebraic sofic shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 15 February 2024, pp. 2859-2900
- Print publication:
- October 2024
-
- Article
- Export citation
5 - Singular Supports
- from Part One - Historical and Theoretical Background
-
- Book:
- The Christoffel–Darboux Kernel for Data Analysis
- Published online:
- 31 March 2022
- Print publication:
- 07 April 2022, pp 61-74
-
- Chapter
- Export citation
2 - Stratified Spaces
-
- Book:
- Singular Intersection Homology
- Published online:
- 18 September 2020
- Print publication:
- 24 September 2020, pp 16-85
-
- Chapter
- Export citation
CHARACTERIZING HERMITIAN VARIETIES IN THREE- AND FOUR-DIMENSIONAL PROJECTIVE SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 29 October 2018, pp. 1-8
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation