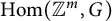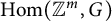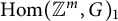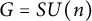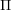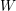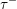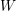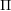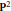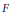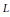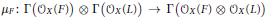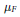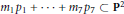Refine search
Actions for selected content:
5 results
Torsion in the space of commuting elements in a Lie group
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 22 May 2023, pp. 1033-1061
- Print publication:
- June 2024
-
- Article
- Export citation
Lattice structure of Weyl groups via representation theory of preprojective algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 6 / June 2018
- Published online by Cambridge University Press:
- 16 May 2018, pp. 1269-1305
- Print publication:
- June 2018
-
- Article
- Export citation
Homological realization of Nakajima varieties and Weyl group actions
-
- Journal:
- Compositio Mathematica / Volume 141 / Issue 6 / November 2005
- Published online by Cambridge University Press:
- 04 December 2007, pp. 1479-1503
- Print publication:
- November 2005
-
- Article
-
- You have access
- Export citation
An Algorithm for Fat Points on
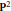 ${{\mathbf{P}}^{2}}$
${{\mathbf{P}}^{2}}$
-
- Journal:
- Canadian Journal of Mathematics / Volume 52 / Issue 1 / 01 February 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 123-140
- Print publication:
- 01 February 2000
-
- Article
-
- You have access
- Export citation
Crystallized structure for level 0 part of modified quantum affine algebra $\tilde{U}_q (\widehat{{\frak s}{\frak l}_2})$
-
- Journal:
- Compositio Mathematica / Volume 108 / Issue 1 / August 1997
- Published online by Cambridge University Press:
- 04 December 2007, pp. 1-33
- Print publication:
- August 1997
-
- Article
-
- You have access
- Export citation