Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-25T20:02:59.533Z Has data issue: false hasContentIssue false
  • English
  • Français

Lattice structure of Weyl groups via representation theory of preprojective algebras

Part of: Special aspects of infinite or finite groups Representation theory of rings and algebras Lattices Abelian categories Algebraic combinatorics

Published online by Cambridge University Press:  16 May 2018

Osamu Iyama ,
Nathan Reading ,
Idun Reiten  and
Hugh Thomas
Osamu Iyama
Affiliation:
Graduate School of Mathematics, Nagoya University, Chikusa-ku, Nagoya, 464-8602, Japan email iyama@math.nagoya-u.ac.jphttp://www.math.nagoya-u.ac.jp/∼iyama/
Nathan Reading
Affiliation:
Department of Mathematics, North Carolina State University, Raleigh, NC 27695-8205, USA email reading@math.ncsu.eduhttp://www4.ncsu.edu/∼nreadin/
Idun Reiten
Affiliation:
Department of Mathematical Sciences, Norges teknisk-naturvitenskapelige universitet, 7491 Trondheim, Norway email idun.reiten@math.ntnu.nohttp://www.ntnu.edu/employees/idun.reiten
Hugh Thomas
Affiliation:
Département de mathématiques, Université du Québec à Montréal, CP 8888, Succursale Centre-Ville, Montréal, QC, H3C 3P8, Canada email hugh.ross.thomas@gmail.comhttp://www.lacim.uqam.ca/∼hugh
Get access Rights & Permissions [Opens in a new window]

Abstract

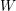This paper studies the combinatorics of lattice congruences of the weak order on a finite Weyl group $W$, using representation theory of the corresponding preprojective algebra 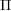$\unicode[STIX]{x1D6F1}$. Natural bijections are constructed between important objects including join-irreducible congruences, join-irreducible (respectively, meet-irreducible) elements of 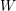$W$, indecomposable $\unicode[STIX]{x1D70F}$-rigid (respectively, 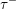$\unicode[STIX]{x1D70F}^{-}$-rigid) modules and layers of 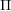$\unicode[STIX]{x1D6F1}$. The lattice-theoretically natural labelling of the Hasse quiver by join-irreducible elements of 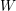$W$ is shown to coincide with the algebraically natural labelling by layers of 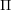$\unicode[STIX]{x1D6F1}$. We show that layers of 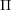$\unicode[STIX]{x1D6F1}$ are nothing but bricks (or equivalently stones, or 2-spherical modules). The forcing order on join-irreducible elements of 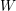$W$ (arising from the study of lattice congruences) is described algebraically in terms of the doubleton extension order. We give a combinatorial description of indecomposable 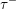$\unicode[STIX]{x1D70F}^{-}$-rigid modules for type 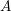$A$ and $D$.

Keywords

preprojective algebraWeyl groupweak order𝜏-tilting theorybrickjoin-irreducible elementlattice congruence

MSC classification

Primary: 16G10: Representations of Artinian rings
Secondary: 05E10: Combinatorial aspects of representation theory 06B10: Ideals, congruence relations 18E40: Torsion theories, radicals 20F55: Reflection and Coxeter groups
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 6 , June 2018 , pp. 1269 - 1305
Copyright
© The Authors 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adachi, T., Iyama, O. and Reiten, I., 𝜏-tilting theory , Compos. Math. 150 (2014), 415–452.Google Scholar
Aihara, T. and Mizuno, Y., Classifying tilting complexes over preprojective algebras of Dynkin type , Algebra Number Theory 11 (2017), 1287–1315.Google Scholar
Amiot, C., Cluster categories for algebras of global dimension 2 and quivers with potential , Ann. Inst. Fourier (Grenoble) 59 (2009), 2525–2590.CrossRefGoogle Scholar
Amiot, C., Iyama, O., Reiten, I. and Todorov, G., Preprojective algebras and c-sortable words , Proc. Lond. Math. Soc. (3) 104 (2012), 513–539.CrossRefGoogle Scholar
Auslander, M. and Smalo, S. O., Almost split sequences in subcategories , J. Algebra 69 (1981), 426–454.Google Scholar
Baer, D., Geigle, W. and Lenzing, H., The preprojective algebra of a tame hereditary Artin algebra , Comm. Algebra 15 (1987), 425–457.Google Scholar
Baumann, P., Kamnitzer, J. and Tingley, P., Affine Mirković–Vilonen polytopes , Publ. Math. Inst. Hautes Études Sci. 120 (2014), 113–205.Google Scholar
Björner, A. and Brenti, F., Combinatorics of Coxeter groups, Graduate Texts in Mathematics, vol. 231 (Springer, New York, 2005).Google Scholar
Bolten, B., Spiegelungsfunktoren für präprojektive Algebren, Diplomarbeit, Bonn (2010).Google Scholar
Bongartz, J., Endotrivial modules over preprojective algebras, Master’s thesis, Bonn (2015).Google Scholar
Buan, A., Iyama, O., Reiten, I. and Scott, J., Cluster structures for 2-Calabi–Yau categories and unipotent groups , Compos. Math. 145 (2009), 1035–1079.Google Scholar
Caspard, N., Le Conte de Poly-Barbut, C. and Morvan, M., Cayley lattices of finite Coxeter groups are bounded , Adv. Appl. Math. 33 (2004), 71–94.Google Scholar
Crawley-Boevey, W. and Holland, M. P., Noncommutative deformations of Kleinian singularities , Duke Math. J. 92 (1998), 605–635.Google Scholar
Day, A., Congruence normality: the characterization of the doubling class of convex sets , Algebra Universalis 31 (1994), 397–406.Google Scholar
Demonet, L., Iyama, O. and Jasso, G., $\unicode[STIX]{x1D70F}$ -tilting finite algebras, bricks and $g$ -vectors, Int. Math. Res. Not. IMRN, to appear. Preprint (2015), arXiv:1503.00285.Google Scholar
Demonet, L., Iyama, O., Reiten, I., Reading, N. and Thomas, H., Lattice theory of torsion classes, Preprint (2017), arXiv:1711.01785.Google Scholar
Dlab, V. and Ringel, C. M., The preprojective algebra of a modulated graph , in Representation theory, II (Proc. Second Internat. Conf., Carleton Univ., Ottawa, Ont., 1979), Lecture Notes in Mathematics, vol. 832 (Springer, Berlin, New York, 1980), 216–231.Google Scholar
Geiss, C., Leclerc, B. and Schröer, J., Kac-Moody groups and cluster algebras , Adv. Math. 228 (2011), 329–433.Google Scholar
Happel, D., Hartlieb, S., Kerner, O. and Unger, L., On perpendicular categories of stones over quiver algebras , Comment. Math. Helv. 71 (1996), 463–474.Google Scholar
Iyama, O. and Reiten, I., Fomin–Zelevinsky mutation and tilting modules over Calabi–Yau algebras , Amer. J. Math. 130 (2008), 1087–1149.CrossRefGoogle Scholar
Iyama, O., Reiten, I., Thomas, H. and Todorov, G., Lattice structure of torsion classes for path algebras , Bull. Lond. Math. Soc. 47 (2015), 639–650.Google Scholar
Kashiwara, M. and Saito, Y., Geometric construction of crystal bases , Duke Math. J. 89 (1997), 9–36.Google Scholar
Keller, B., Calabi–Yau triangulated categories , in Trends in representation theory of algebras and related topics, EMS Ser. Congr. Rep. (Eur. Math. Soc., Zürich, 2008), 467–489.Google Scholar
Kerner, O. and Lukas, F., Regular stones of wild hereditary algebras , J. Pure Appl. Algebra 93 (1994), 15–31.Google Scholar
Kimura, Y., Tilting theory of preprojective algebras and c-sortable elements , J. Algebra 503 (2018), 186–221.Google Scholar
Leclerc, B., Cluster structures on strata of flag varieties , Adv. Math. 300 (2016), 190–228.Google Scholar
Lusztig, G., Quivers, perverse sheaves, and quantized enveloping algebras , J. Amer. Math. Soc. 4 (1991), 365–421.Google Scholar
Marks, F., Homological embeddings for preprojective algebras , Math. Z. 285 (2017), 1091–1106.Google Scholar
Mizuno, Y., Classifying 𝜏-tilting modules over preprojective algebras of Dynkin type , Math. Z. 277 (2014), 665–690.Google Scholar
Nakajima, H., Instantons on ALE spaces, quiver varieties, and Kac–Moody algebras , Duke Math. J. 76 (1994), 365–416.Google Scholar
Oppermann, S., Reiten, I. and Thomas, H., Quotient closed subcategories of quiver representations , Compos. Math. 151 (2015), 568–602.Google Scholar
Reading, N., Lattice congruences of the weak order , Order 21 (2004), 315–344.Google Scholar
Reading, N., Lattice theory of the poset of regions , in Lattice theory: special topics and applications, Vol. 2 (Birkhäuser/Springer, Cham, 2016), 399–487.Google Scholar
Reading, N., Finite Coxeter groups and the weak order , in Lattice theory: special topics and applications, Vol. 2 (Birkhäuser/Springer, Cham, 2016), 489–561.Google Scholar
Ringel, C. M., Representations of K-species and bimodules , J. Algebra 41 (1976), 269–302.Google Scholar
Smalø, S. O., Torsion theories and tilting modules , Bull. Lond. Math. Soc. 16 (1984), 518–522.CrossRefGoogle Scholar
Seidel, P. and Thomas, R., Braid group actions on derived categories of coherent sheaves , Duke Math. J 108 (2001), 37–108.Google Scholar
Sekiya, Y. and Yamaura, K., Tilting theoretical approach to moduli spaces over preprojective algebras , Algebr. Represent. Theory 16 (2013), 1733–1786.Google Scholar
Wald, B. and Waschbüsch, J., Tame biserial algebras , J. Algebra 95 (1985), 480–500.Google Scholar