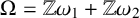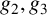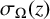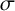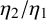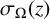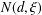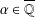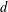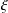Refine search
Actions for selected content:
6 results
A new way to tackle a conjecture of Rémond
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 31 October 2023, pp. 2049-2072
- Print publication:
- December 2024
-
- Article
- Export citation
ON THE NUMBER OF ALGEBRAIC POINTS ON THE GRAPH OF THE WEIERSTRASS SIGMA FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 13 January 2023, pp. 205-216
- Print publication:
- October 2023
-
- Article
- Export citation
POINTS OF SMALL HEIGHT ON AFFINE VARIETIES DEFINED OVER FUNCTION FIELDS OF FINITE TRANSCENDENCE DEGREE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 418-427
- Print publication:
- June 2021
-
- Article
- Export citation
ALGEBRAIC NUMBERS WITH BOUNDED DEGREE AND WEIL HEIGHT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 18 July 2018, pp. 212-220
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
IRRATIONALITY AND NONQUADRATICITY MEASURES FOR LOGARITHMS OF ALGEBRAIC NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 22 November 2012, pp. 237-267
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
The Infimum in the Metric Mahler Measure
-
- Journal:
- Canadian Mathematical Bulletin / Volume 54 / Issue 4 / 01 December 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 739-747
- Print publication:
- 01 December 2011
-
- Article
-
- You have access
- Export citation