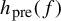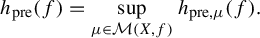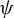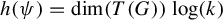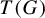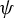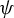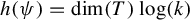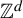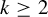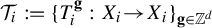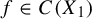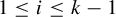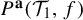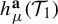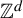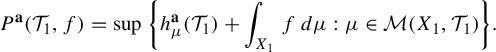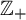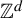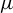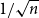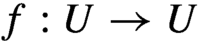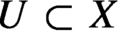Refine search
Actions for selected content:
29 results
Variational principles of metric mean dimension for random dynamical systems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 18 September 2025, pp. 1-25
-
- Article
-
- You have access
- HTML
- Export citation
A variational principle of scaled entropy for amenable group actions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-28
-
- Article
- Export citation
Entropy of group actions beyond uniform lattices
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 21 November 2024, pp. 1461-1502
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A variational principle of amenable random metric mean dimensions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 16 May 2024, pp. 852-875
-
- Article
- Export citation
Weighted topological pressure revisited
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 08 May 2024, pp. 34-70
- Print publication:
- January 2025
-
- Article
- Export citation
3 - The Time-Independent Schrödinger Equation
-
- Book:
- A Computational Introduction to Quantum Physics
- Published online:
- 24 April 2024
- Print publication:
- 25 April 2024, pp 37-56
-
- Chapter
- Export citation
Project 8: - Cylindrical Capacitor
-
- Book:
- A First Guide to Computational Modelling in Physics
- Published online:
- 01 February 2024
- Print publication:
- 08 February 2024, pp 52-56
-
- Chapter
- Export citation
A note on preimage entropy
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 19 June 2023, pp. 1468-1472
- Print publication:
- May 2024
-
- Article
- Export citation
6 - Measure-Theoretic Entropy
- from Part I - Ergodic Theory and Geometric Measures
-
- Book:
- Meromorphic Dynamics
- Published online:
- 20 April 2023
- Print publication:
- 04 May 2023, pp 160-191
-
- Chapter
- Export citation
The topological entropy of powers on Lie groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 13 December 2022, pp. 3726-3744
- Print publication:
- November 2023
-
- Article
- Export citation
1 - Elements of Operator Theory
- from Part One - Background Material
-
- Book:
- Schrödinger Operators: Eigenvalues and Lieb–Thirring Inequalities
- Published online:
- 03 November 2022
- Print publication:
- 17 November 2022, pp 7-65
-
- Chapter
- Export citation
A variational principle for weighted topological pressure under
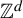 $\mathbb {Z}^{d}$-actions
$\mathbb {Z}^{d}$-actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 04 October 2022, pp. 3311-3340
- Print publication:
- October 2023
-
- Article
- Export citation
New approach to weighted topological entropy and pressure
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 28 January 2022, pp. 1004-1034
- Print publication:
- March 2023
-
- Article
- Export citation
Packing topological entropy for amenable group actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 20 October 2021, pp. 480-514
- Print publication:
- February 2023
-
- Article
- Export citation
Asymptotics for the number of standard tableaux of skew shape and for weighted lozenge tilings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 18 October 2021, pp. 550-573
-
- Article
- Export citation
Chapter 3 - Space, Time, and Gravity in Newtonian Physics
- from Part I - Space and Time in Newtonian Physics and Special Relativity
-
- Book:
- Gravity
- Published online:
- 03 September 2021
- Print publication:
- 24 June 2021, pp 31-46
-
- Chapter
- Export citation
Strong submeasures and applications to non-compact dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 14 December 2020, pp. 287-309
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
3 - The Variational Principle
- from Part I
-
- Book:
- Modern Classical Mechanics
- Published online:
- 30 November 2020
- Print publication:
- 10 December 2020, pp 119-152
-
- Chapter
- Export citation
On preimage entropy, folding entropy and stable entropy
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 14 January 2020, pp. 1217-1249
- Print publication:
- April 2021
-
- Article
- Export citation
12 - Energy Methods
- from Part II - Applications
-
- Book:
- Intermediate Solid Mechanics
- Published online:
- 16 December 2019
- Print publication:
- 09 January 2020, pp 386-437
-
- Chapter
- Export citation