No CrossRef data available.
Article contents
Strong submeasures and applications to non-compact dynamical systems
Published online by Cambridge University Press: 14 December 2020
Abstract
A strong submeasure on a compact metric space X is a sub-linear and bounded operator on the space of continuous functions on X. A strong submeasure is positive if it is non-decreasing. By the Hahn–Banach theorem, a positive strong submeasure is the supremum of a non-empty collection of measures whose masses are uniformly bounded from above. There are many natural examples of continuous maps of the form 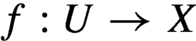 $f:U\rightarrow X$, where X is a compact metric space and
$f:U\rightarrow X$, where X is a compact metric space and 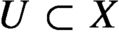 $U\subset X$ is an open-dense subset, where f cannot extend to a reasonable function on X. We can mention cases such as transcendental maps of
$U\subset X$ is an open-dense subset, where f cannot extend to a reasonable function on X. We can mention cases such as transcendental maps of 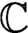 $\mathbb {C}$, meromorphic maps on compact complex varieties, or continuous self-maps
$\mathbb {C}$, meromorphic maps on compact complex varieties, or continuous self-maps 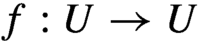 $f:U\rightarrow U$ of a dense open subset
$f:U\rightarrow U$ of a dense open subset 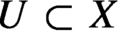 $U\subset X$ where X is a compact metric space. For the aforementioned mentioned the use of measures is not sufficient to establish the basic properties of ergodic theory, such as the existence of invariant measures or a reasonable definition of measure-theoretic entropy and topological entropy. In this paper we show that strong submeasures can be used to completely resolve the issue and establish these basic properties. In another paper we apply strong submeasures to the intersection of positive closed
$U\subset X$ where X is a compact metric space. For the aforementioned mentioned the use of measures is not sufficient to establish the basic properties of ergodic theory, such as the existence of invariant measures or a reasonable definition of measure-theoretic entropy and topological entropy. In this paper we show that strong submeasures can be used to completely resolve the issue and establish these basic properties. In another paper we apply strong submeasures to the intersection of positive closed 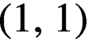 $(1,1)$ currents on compact Kähler manifolds.
$(1,1)$ currents on compact Kähler manifolds.
Keywords
MSC classification
Information
- Type
- Original Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press


