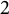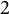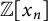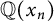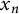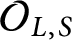Refine search
Actions for selected content:
3 results
On the root of unity ambiguity in a formula for the Brumer–Stark units
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 27 December 2023, pp. 611-623
- Print publication:
- September 2024
-
- Article
- Export citation
A dynamical characterization for monogenity at every level of some infinite
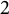 $2$-towers
$2$-towers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 20 October 2021, pp. 806-814
- Print publication:
- September 2022
-
- Article
- Export citation
Finite descent obstruction for Hilbert modular varieties
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 22 July 2020, pp. 452-473
- Print publication:
- June 2021
-
- Article
- Export citation