In this paper, we compute the LS-category and equivariant LS-category of a small cover and its real moment angle manifold. We calculate a tight lower bound for the topological complexity of many small covers over a product of simplices. Then we compute symmetric topological complexity of several small covers over a product of simplices. We calculate the LS one-category of real Bott manifolds and infinitely many small covers.

There is a problem with the proofs of [1], Lemma 4.4 and the related Theorems 4.5, 4.8 and 4.12 regarding the computation of zero-divisor cup-length of real Grassmann manifolds ${G_k({{\mathbb {R}}}^{n})}$. The correct statements and improved estimates of the topological complexity of ${G_k({{\mathbb {R}}}^{n})}$ will appear in a separate paper by M. Radovanović [2].

Topological complexity naturally appears in the motion planning in robotics. In this paper we consider the problem of finding topological complexity of real Grassmann manifolds $G_k(\mathbb {R}^{n})$. We use cohomology methods to give estimates on the zero-divisor cup-length of $G_k(\mathbb {R}^{n})$ for various $2\leqslant k< n$, which in turn give us lower bounds on topological complexity. Our results correct and improve several results from Pavešić (Proc. Roy. Soc. Edinb. A 151 (2021), 2013–2029).

For a graph $\Gamma$, let $K(H_{\Gamma },\,1)$ denote the Eilenberg–Mac Lane space associated with the right-angled Artin (RAA) group $H_{\Gamma }$ defined by $\Gamma$. We use the relationship between the combinatorics of $\Gamma$ and the topological complexity of $K(H_{\Gamma },\,1)$ to explain, and generalize to the higher TC realm, Dranishnikov's observation that the topological complexity of a covering space can be larger than that of the base space. 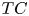In the process, for any positive integer $n$, we construct a graph $\mathcal {O}_n$ whose TC-generating function has polynomial numerator of degree $n$. Additionally, motivated by the fact that $K(H_{\Gamma },\,1)$ can be realized as a polyhedral product, we study the LS category and topological complexity of more general polyhedral product spaces. In particular, we use the concept of a strong axial map in order to give an estimate, sharp in a number of cases, of the topological complexity of a polyhedral product whose factors are real projective spaces. Our estimate exhibits a mixed cat-TC phenomenon not present in the case of RAA groups.

We use some detailed knowledge of the cohomology ring of real Grassmann manifolds Gk(ℝn) to compute zero-divisor cup-length and estimate topological complexity of motion planning for k-linear subspaces in ℝn. In addition, we obtain results about monotonicity of Lusternik–Schnirelmann category and topological complexity of Gk(ℝn) as a function of n.

In robotics, a topological theory of motion planning was initiated by M. Farber. We present optimal motion planning algorithms which can be used in designing practical systems controlling objects moving in Euclidean space without collisions between them and avoiding obstacles. Furthermore, we present the multi-tasking version of the algorithms.

The Lusternik–Schnirelmann categorycat and topological complexityTC are related homotopy invariants. The topological complexityTC has applications to the robot motion planning problem. We calculate the Lusternik–Schnirelmann category and topological complexity of the ordered configuration space 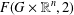of two distinct points in the product $G\times \mathbb{R}^{n}$ and apply the results to the planar and spatial motion of two rigid bodies in $\mathbb{R}^{2}$ and $\mathbb{R}^{3}$ respectively.

An n-dimensional analogue of the Klein bottle arose in our study of topological complexity of planar polygon spaces. We determine its integral cohomology algebra and stable homotopy type, and give an explicit immersion and embedding in Euclidean space.

This work is motivated by the question of whether there are spaces X for which the Farber–Grant symmetric topological complexity TCS(X) differs from the Basabe–González–Rudyak–Tamaki symmetric topological complexity TCΣ(X). For a projective space ${\open R}\hbox{P}^m$, it is known that $\hbox{TC}^S ({\open R}\hbox{P}^{m})$ captures, with a few potential exceptional cases, the Euclidean embedding dimension of ${\open R}\hbox{P}^{m}$. We now show that, for all m≥1, $\hbox{TC}^{\Sigma}({\open R}\hbox{P}^{m})$ is characterized as the smallest positive integer n for which there is a symmetric ${\open Z}_{2}$-biequivariant map Sm×Sm→Sn with a ‘monoidal’ behaviour on the diagonal. This result thus lies at the core of the efforts in the 1970s to characterize the embedding dimension of real projective spaces in terms of the existence of symmetric axial maps. Together with Nakaoka's description of the cohomology ring of symmetric squares, this allows us to compute both TC numbers in the case of ${\open R}\hbox{P}^{2^{e}}$ for e≥1. In particular, this leaves the torus S1×S1 as the only closed surface whose symmetric (symmetrized) TCS (TCΣ) invariant is currently unknown.

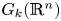
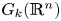
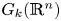
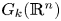
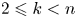
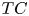
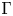
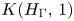
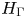
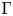
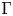
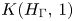
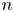
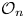
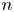
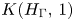
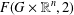
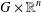
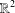
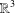
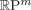
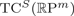
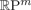
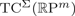
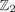
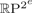
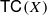The topological complexity is a numerical homotopy invariant of a topological space 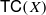X which is motivated by robotics and is similar in spirit to the classical Lusternik–Schnirelmann category of X. Given a mechanical system with configuration space X, the invariant measures the complexity of motion planning algorithms which can be designed for the system. In this paper, we compute the topological complexity of the configuration space of n distinct ordered points on an orientable surface, for both closed and punctured surfaces. Our main tool is a theorem of B. Totaro describing the cohomology of configuration spaces of algebraic varieties. For configuration spaces of punctured surfaces, this is used in conjunction with techniques from the theory of mixed Hodge structures.

An almost-direct product of free groups is an iterated semidirect product of finitely generated free groups in which the action of the constituent free groups on the homology of one another is trivial. We determine the structure of the cohomology ring of such a group. This is used to analyze the topological complexity of the associated Eilenberg–MacLane space.