Refine search
Actions for selected content:
13 results
Infinitesimal Hilbertianity of Weighted Riemannian Manifolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 27 September 2019, pp. 118-140
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
Pointwise Characterizations of Even Order Sobolev Spaces via Derivatives of Ball Averages
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 15 October 2018, pp. 681-699
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Sobolev Algebras Through a ‘Carré Du Champ’ Identity
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 24 July 2018, pp. 1041-1054
-
- Article
- Export citation
Littlewood–Paley characterizations of fractional Sobolev spaces via averages on balls
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 22 June 2018, pp. 1135-1163
- Print publication:
- December 2018
-
- Article
- Export citation
Eigenvalues of −Δp − Δq Under Neumann Boundary Condition
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 3 / 01 September 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 606-616
- Print publication:
- 01 September 2016
-
- Article
-
- You have access
- Export citation
Littlewood–Paley Characterizations of Second-Order Sobolev Spaces via Averages on Balls
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 1 / 01 March 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 104-118
- Print publication:
- 01 March 2016
-
- Article
-
- You have access
- Export citation
Controllability problems for the 1-D wave equation on ahalf-axis with the Dirichlet boundary control
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 3 / July 2012
- Published online by Cambridge University Press:
- 19 September 2011, pp. 748-773
- Print publication:
- July 2012
-
- Article
- Export citation
REGULARITY OF SOLUTIONS TO A TIME-FRACTIONAL DIFFUSION EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 52 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 18 July 2011, pp. 123-138
-
- Article
-
- You have access
- Export citation
THE DECAY OF THE WALSH COEFFICIENTS OF SMOOTH FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 02 July 2009, pp. 430-453
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
LOCAL RADIAL BASIS FUNCTION APPROXIMATION ON THE SPHERE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 197-224
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
Hardy Space Estimate for the Product of Singular Integrals
-
- Journal:
- Canadian Journal of Mathematics / Volume 52 / Issue 2 / 01 April 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 381-411
- Print publication:
- 01 April 2000
-
- Article
-
- You have access
- Export citation
Constrained Approximation in Sobolev Spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 49 / Issue 1 / 01 February 1997
- Published online by Cambridge University Press:
- 20 November 2018, pp. 74-99
- Print publication:
- 01 February 1997
-
- Article
-
- You have access
- Export citation
Regularity of mean-values
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 1 / August 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 117-126
- Print publication:
- August 1988
-
- Article
-
- You have access
- Export citation
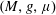
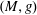
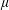
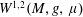
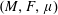
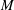
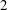
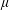
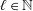
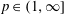
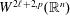
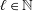
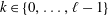
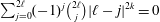
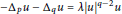
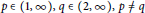
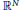
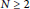
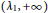
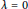
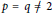
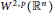
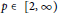
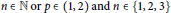
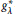
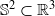 . More precisely, we consider radial basis function interpolation based on data on a (global or local) point set
. More precisely, we consider radial basis function interpolation based on data on a (global or local) point set 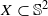 for functions in the Sobolev space
for functions in the Sobolev space 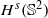 with norm
with norm 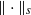 , where
, where 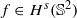 satisfies
satisfies 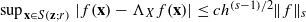 , where
, where 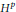
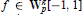 are considered. Both uniform and pointwise estimates, which are exact in some sense, are obtained.
are considered. Both uniform and pointwise estimates, which are exact in some sense, are obtained.