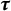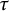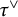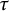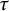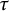Refine search
Actions for selected content:
5 results
On infinitesimal
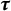 $\boldsymbol { \tau }$-isospectrality of locally symmetric spaces
$\boldsymbol { \tau }$-isospectrality of locally symmetric spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 246-261
- Print publication:
- March 2025
-
- Article
- Export citation
12 - String amplitudes
- from Part II - Extensions and applications
-
- Book:
- Modular Forms and String Theory
- Published online:
- 28 November 2024
- Print publication:
- 12 December 2024, pp 223-258
-
- Chapter
- Export citation
Geometric orbital integrals and the center of the enveloping algebra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 11 August 2022, pp. 1189-1253
- Print publication:
- June 2022
-
- Article
- Export citation
Adiabatic limit of the eta invariant over cofinite quotients of PSL(2, ℝ)
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 6 / November 2008
- Published online by Cambridge University Press:
- 26 September 2008, pp. 1593-1616
- Print publication:
- November 2008
-
- Article
-
- You have access
- Export citation
On Limit Multiplicities for Spaces of Automorphic Forms
-
- Journal:
- Canadian Journal of Mathematics / Volume 51 / Issue 5 / 01 October 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 952-976
- Print publication:
- 01 October 1999
-
- Article
-
- You have access
- Export citation