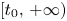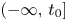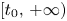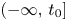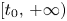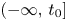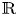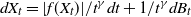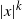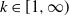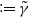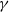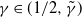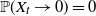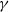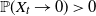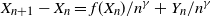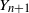Refine search
Actions for selected content:
43 results
(Empirical) Gramian-based dimension reduction for stochastic differential equations driven by fractional Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 07 November 2025, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
1 - Background
-
- Book:
- Scalable Monte Carlo for Bayesian Learning
- Published online:
- 16 May 2025
- Print publication:
- 05 June 2025, pp 1-38
-
- Chapter
-
- You have access
- Export citation
How to beat a Bayesian adversary
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 28 March 2025, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zero-Inflated Regime-Switching Stochastic Differential Equation Models for Highly Unbalanced Multivariate, Multi-Subject Time-Series Data
-
- Journal:
- Psychometrika / Volume 84 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 01 January 2025, pp. 611-645
-
- Article
- Export citation
ON MODELLING WATER QUALITY WITH STOCHASTIC DIFFERENTIAL EQUATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 65 / Issue 3 / July 2023
- Published online by Cambridge University Press:
- 09 January 2024, pp. 273-284
-
- Article
-
- You have access
- HTML
- Export citation
2 - Dynamical Systems and Markov Processes
- from Part I - Concepts from Modeling, Inference, and Computing
-
- Book:
- Data Modeling for the Sciences
- Published online:
- 17 August 2023
- Print publication:
- 31 August 2023, pp 40-107
-
- Chapter
- Export citation
ESSAYS ON STRONG AND WEAK APPROXIMATIONS OF STOCHASTIC DIFFERENTIAL EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 16 June 2023, pp. 175-176
- Print publication:
- August 2023
-
- Article
-
- You have access
- HTML
- Export citation
Robustness of nonuniform mean-square exponential dichotomies
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 18 April 2023, pp. 525-567
- Print publication:
- April 2024
-
- Article
- Export citation
Diffusion approximation of multi-class Hawkes processes: Theoretical and numerical analysis
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 October 2021, pp. 716-756
- Print publication:
- September 2021
-
- Article
- Export citation
6 - Connections between Stochastic Differential Equations and Partial Integro-Differential Equations
- from Part I - Point Processes
-
- Book:
- Point Processes and Jump Diffusions
- Published online:
- 27 May 2021
- Print publication:
- 17 June 2021, pp 56-63
-
- Chapter
- Export citation
One-dimensional system arising in stochastic gradient descent
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 01 July 2021, pp. 575-607
- Print publication:
- June 2021
-
- Article
- Export citation
3 - Stochastic Differential Equations
-
- Book:
- Stochastic Modelling of Reaction–Diffusion Processes
- Published online:
- 04 November 2019
- Print publication:
- 30 January 2020, pp 59-94
-
- Chapter
- Export citation

Stochastic Modelling of Reaction–Diffusion Processes
-
- Published online:
- 04 November 2019
- Print publication:
- 30 January 2020
Approximate analytical solutions for a class of nonlinear stochastic differential equations
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 18 September 2018, pp. 928-944
-
- Article
- Export citation
Targeted energy transfer in stochastically excited system with nonlinear energy sink
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 18 September 2018, pp. 869-886
-
- Article
- Export citation
STOCHASTIC MODELS FOR OPTICALLY TRAPPED NANOWIRES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 30 May 2018, pp. 343-344
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
Differential Equations Driven by Π-Rough Paths
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 21 January 2016, pp. 741-758
-
- Article
- Export citation
Stochastic Models for Chladni Figures
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 10 August 2015, pp. 287-300
-
- Article
- Export citation
Measuring the Irreversibility of Numerical Schemes forReversible Stochastic Differential Equations∗
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 5 / September 2014
- Published online by Cambridge University Press:
- 13 August 2014, pp. 1351-1379
- Print publication:
- September 2014
-
- Article
- Export citation
STATISTICAL CAUSALITY AND MARTINGALE REPRESENTATION PROPERTY WITH APPLICATION TO STOCHASTIC DIFFERENTIAL EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 20 May 2014, pp. 327-338
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation