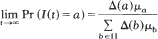Refine search
Actions for selected content:
1 results
An invariance principle for semi-Markov processes
-
- Journal:
- Advances in Applied Probability / Volume 17 / Issue 1 / March 1985
- Published online by Cambridge University Press:
- 01 July 2016, pp. 100-126
- Print publication:
- March 1985
-
- Article
- Export citation
-
Let (I(t))∞ t = () be a semi-Markov process with state space II and recurrent probability transition kernel P. Subject to certain mixing conditions,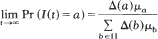
where Δis an invariant probability measure for P and μb is the expected sojourn time in state b ϵΠ. We show that this limit is robust; that is, for each state b ϵ Πthe sojourn-time distribution may change for each transition, but, as long as the expected sojourn time in b is µb on the average, the above limit still holds. The kernel P may also vary for each transition as long as Δis invariant.
