No CrossRef data available.
Article contents
An invariance principle for semi-Markov processes
Published online by Cambridge University Press: 01 July 2016
Abstract
Let (I(t))∞ t = () be a semi-Markov process with state space II and recurrent probability transition kernel P. Subject to certain mixing conditions,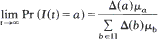 where Δis an invariant probability measure for P and μb is the expected sojourn time in state b ϵΠ. We show that this limit is robust; that is, for each state b ϵ Πthe sojourn-time distribution may change for each transition, but, as long as the expected sojourn time in b is µb on the average, the above limit still holds. The kernel P may also vary for each transition as long as Δis invariant.
where Δis an invariant probability measure for P and μb is the expected sojourn time in state b ϵΠ. We show that this limit is robust; that is, for each state b ϵ Πthe sojourn-time distribution may change for each transition, but, as long as the expected sojourn time in b is µb on the average, the above limit still holds. The kernel P may also vary for each transition as long as Δis invariant.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Applied Probability Trust 1985
Footnotes
Research supported by the National Research Council of Canada.
References
1. Arjas, E., Nummelin, E. and Tweedie, R. (1978) Uniform limit theorems for non-singular renewal and Markov renewal processes.
J. Appl. Prob.
15, 112–125.CrossRefGoogle Scholar
2. Berbee, H. C. P. (1979)
Random Walks with Stationary Increments and Renewal Theory.
Mathematical Center Tracts, Amsterdam.Google Scholar
3. Dobrushin, R. L. (1956) Central limit theorems for non-stationary Markov chains.
Theory Prob. Appl.
1, 65–80.CrossRefGoogle Scholar
5. Mcdonald, D. (1978) On semi-Markov and semi-regenerative processes I.
Z. Wahrscheinlichkeitsth.
42, 261–277.CrossRefGoogle Scholar
6. Mcdonald, D. (1978) On semi-Markov and semi-regenerative processes II.
Ann. Prob.
6, 995–1014.CrossRefGoogle Scholar
7. Mcdonald, D. (1979) Ergodic behaviour of nonstationary regenerative processes.
Trans. Amer. Math. Soc.
255, 135–152.CrossRefGoogle Scholar
8. Pitman, J. W. (1974) Uniform rates of convergence for Markov chain transition probabilities.
Z. Wahrscheinlichkeitsth.
29, 193–227.CrossRefGoogle Scholar

