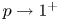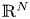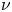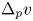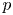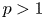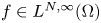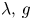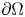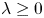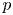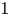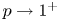Refine search
Actions for selected content:
7 results
Steady-state solutions for a reaction–diffusion equation with Robin boundary conditions: Application to the control of dengue vectors
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 18 September 2023, pp. 382-408
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Behaviour of solutions to p-Laplacian with Robin boundary conditions as p goes to 1
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 26 January 2023, pp. 105-130
- Print publication:
- February 2024
-
- Article
- Export citation
PDE comparison principles for Robin problems
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 23 September 2021, pp. 108-139
- Print publication:
- February 2023
-
- Article
- Export citation
Corrigendum to: Dirichlet and Neumann boundary conditions for the p-Laplace operator: What is in between?
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1689-1691
- Print publication:
- December 2019
-
- Article
- Export citation
Efficient Chebyshev Spectral Method for Solving Linear Elliptic PDEs Using Quasi-Inverse Technique
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 4 / Issue 2 / May 2011
- Published online by Cambridge University Press:
- 28 May 2015, pp. 197-215
- Print publication:
- May 2011
-
- Article
- Export citation
A Least-Squares/Fictitious Domain Method for Linear Elliptic Problems with Robin Boundary Conditions
-
- Journal:
- Communications in Computational Physics / Volume 9 / Issue 3 / March 2011
- Published online by Cambridge University Press:
- 20 August 2015, pp. 587-606
- Print publication:
- March 2011
-
- Article
- Export citation
ON THE ISOPERIMETRIC PROBLEM FOR THE LAPLACIAN WITH ROBIN AND WENTZELL BOUNDARY CONDITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 16 August 2010, pp. 348-350
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation