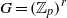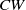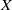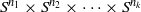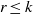Refine search
Actions for selected content:
7 results
FREE ACTIONS OF SOME COMPACT GROUPS ON MILNOR MANIFOLDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 31 October 2018, pp. 727-742
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Strong cohomological rigidity of toric varieties
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 5 / October 2017
- Published online by Cambridge University Press:
- 25 September 2017, pp. 971-992
- Print publication:
- October 2017
-
- Article
- Export citation
ON ALGEBRAIC INVARIANTS FOR FREE ACTIONS ON HOMOTOPY SPHERES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 04 September 2015, pp. 478-487
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Classification of Bott Manifolds up to Dimension 8
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 3 / October 2015
- Published online by Cambridge University Press:
- 10 December 2014, pp. 653-659
-
- Article
-
- You have access
- Export citation
Fusion systems and group actions with abelian isotropy subgroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 3 / October 2013
- Published online by Cambridge University Press:
- 10 July 2013, pp. 873-886
-
- Article
-
- You have access
- Export citation
A NOTE ON FREE ACTIONS OF GROUPS ON PRODUCTS OF SPHERES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 08 March 2013, pp. 340-344
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
Free Actions of Abelian Groups on a Cartesian Power of an Even Sphere
-
- Journal:
- Canadian Mathematical Bulletin / Volume 30 / Issue 3 / 01 September 1987
- Published online by Cambridge University Press:
- 20 November 2018, pp. 358-362
- Print publication:
- 01 September 1987
-
- Article
-
- You have access
- Export citation
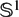
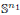 × … ×
× … × 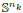 for some positive integers
for some positive integers