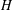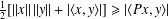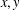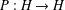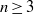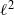Refine search
Actions for selected content:
5 results
BUZANO’S INEQUALITY HOLDS FOR ANY PROJECTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 20 January 2016, pp. 504-510
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
AN EXAMPLE CONCERNING BOUNDED LINEAR REGULARITY OF SUBSPACES IN HILBERT SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 12 September 2013, pp. 217-226
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
THE STATE-SPACE OF THE LATTICE OF ORTHOGONALLY CLOSED SUBSPACES
-
- Journal:
- Glasgow Mathematical Journal / Volume 47 / Issue 1 / January 2005
- Published online by Cambridge University Press:
- 31 January 2005, pp. 213-220
- Print publication:
- January 2005
-
- Article
-
- You have access
- Export citation
ON A PROPERTY OF BASES IN A HILBERT SPACE
-
- Journal:
- Glasgow Mathematical Journal / Volume 46 / Issue 1 / January 2004
- Published online by Cambridge University Press:
- 15 January 2004, pp. 177-180
- Print publication:
- January 2004
-
- Article
-
- You have access
- Export citation
An algebraic approach to Wigner's unitary-antiunitary theorem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 3 / December 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 354-369
- Print publication:
- December 1998
-
- Article
-
- You have access
- Export citation