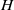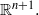Refine search
Actions for selected content:
7 results
Adjoint Orbits of Semi-Simple Lie Groups and Lagrangian Submanifolds
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 15 June 2016, pp. 361-385
-
- Article
- Export citation
SUPERBOSONIZATION VIA RIESZ SUPERDISTRIBUTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 14 May 2014, e9
-
- Article
-
- You have access
- Open access
- Export citation
UNIQUENESS OF SOLUTIONS TO SCHRÖDINGER EQUATIONS ON
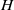 $H$-TYPE GROUPS
$H$-TYPE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 07 August 2013, pp. 297-314
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
TOWARDS DIFFERENTIAL CALCULUS IN STRATIFIED GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 17 June 2013, pp. 76-128
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
A PALEY–WIENER THEOREM FOR DISTRIBUTIONS ON REDUCTIVE SYMMETRIC SPACES
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 6 / Issue 4 / October 2007
- Published online by Cambridge University Press:
- 28 November 2006, pp. 557-577
- Print publication:
- October 2007
-
- Article
- Export citation
Estimates for kernels of intertwining operators on SL(n, R)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 1 / August 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 105-120
- Print publication:
- August 2006
-
- Article
-
- You have access
- Export citation
Some regularity estimates for convolution semigroups on a group of polynomial growth
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 249-268
- Print publication:
- October 2004
-
- Article
-
- You have access
- Export citation