We provide a concrete example of a normal basis for a finite Galois extension which is not abelian. More precisely, let $\mathbb{C}(X(N))$ be the field of meromorphic functions on the modular curve $X(N)$ of level $N$. We construct a completely free element in the extension $\mathbb{C}(X(N))/\mathbb{C}(X(1))$ by means of Siegel functions.

It is well known that every elliptic curve over the rationals admits a parametrization by means of modular functions. In this short note, we show that only finitely many elliptic curves over $\mathbf{Q}$ can be parametrized by modular units. This answers a question raised by W. Zudilin in a recent work on Mahler measures. Further, we give the list of all elliptic curves $E$ of conductor up to 1000 parametrized by modular units supported in the rational torsion subgroup of $E$. Finally, we raise several open questions.

In a recent paper, Soundararajan has proved the quantum unique ergodicity conjecture by getting a suitable estimate for the second order moment of the so-called ‘Hecke multiplicative’ functions. In the process of proving this he has developed many beautiful ideas. In this paper we generalize his arguments to a general $k$th power and provide an analogous estimate for the $k$th power moment of the Hecke multiplicative functions. This may be of general interest.

Let f be a non-zero cusp form with real Fourier coefficients a(n) (n ≥ 1) of positive real weight k and a unitary multiplier system v on a subgroup Γ ⊂ SL2(ℝ) that is finitely generated and of Fuchsian type of the first kind. Then, it is known that the sequence (a(n))(n ≥ 1) has infinitely many sign changes. 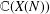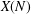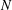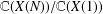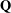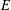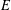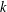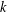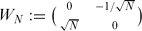In this short note, we generalise the above result to the case of entire modular integrals of non-positive integral weight k on the group Γ0*(N) (N ∈ ℕ) generated by the Hecke congruence subgroup Γ0(N) and the Fricke involution provided that the associated period functions are polynomials.

An AF-algebra is assigned to each cusp form f of weight 2; we study properties of this operator algebra when f is a Hecke eigenform.