The existence and multiplicity of T-periodic solutions to a class of differential equations with attractive singularities at the origin are investigated in the paper. The approach is based on a new method of construction of strict upper and lower functions. The multiplicity results of Ambrosetti–Prodi type are established using a priori estimates and certain properties of topological degree.

This paper is concerned with the periodic (in time) solutions to an one-dimensional semilinear wave equation with x-dependent coefficients. Such a model arises from the forced vibrations of a nonhomogeneous string and propagation of seismic waves in nonisotropic media. By combining variational methods with saddle point reduction technique, we obtain the existence of at least three periodic solutions whenever the period is a rational multiple of the length of the spatial interval. Our method is based on a delicate analysis for the asymptotic character of the spectrum of the wave operator with x-dependent coefficients, and the spectral properties play an essential role in the proof.

As a consequence of the main result of this paper efficient conditions guaranteeing the existence of a T −periodic solution to the second-order differential equation

$${u}^{\prime \prime} = \displaystyle{{h(t)} \over {u^\lambda }}$$

We study the existence and multiplicity of periodic weak solutions for a non-local equation involving an odd subcritical nonlinearity which is asymptotically linear at infinity. We investigate such problem by applying the pseudo-index theory developed by Bartolo, Benci and Fortunato [11] after transforming the problem to a degenerate elliptic problem in a half-cylinder with a Neumann boundary condition, via a Caffarelli-Silvestre type extension in periodic setting. The periodic nonlocal case, considered here, presents, respect to the cases studied in the literature, some new additional difficulties and a careful analysis of the fractional spaces involved is necessary.

Using the Leray–Schauder degree, we study the existence of solutions for the following periodic differential equation with relativistic acceleration and singular nonlinearity:

where μ > 1 and the weight h: [0, T] → ℝ is a continuous sign-changing function. There are no a priori estimates on the set of positive solutions (a condition used in general to apply the Leray–Schauder degree), and we prove that no solution of the equation appears on the boundary of an unbounded open set during the deformation to an autonomous problem.

Using a variational approach we obtain the existence of at least three periodic solutions for discontinuous perturbations of the vector p-Laplacian operator .

A modified predator-prey system described by two differential equations and an algebraic equation is discussed. Formulae for determining the direction of a Hopf bifurcation and the stability of the bifurcating periodic solutions are derived differential-algebraic system theory, bifurcation theory and centre manifold theory. Numerical simulations illustrate the results, which includes quite complex dynamical behaviour.

The aim of this paper is to give a detailed analysis of Hopf bifurcation of a ratio-dependent predator–prey system involving two discrete delays. A delay parameter is chosen as the bifurcation parameter for the analysis. Stability of the bifurcating periodic solutions is determined by using the centre manifold theorem and the normal form theory introduced by Hassard et al. Some of the bifurcation properties including the direction, stability and period are given. Finally, our theoretical results are supported by some numerical simulations.

In this paper we study the existence of periodic solutions of a Volterra type integral equation with infinite heredity. Banach fixed point theorem, Krasnosel'skii's fixed point theorem, and a combination of Krasnosel'skii's and Schaefer's fixed point theorems are employed in the analysis. The combination theorem of Krasnosel'skii and Schaefer requires an a priori bound on all solutions. We employ Liapunov's direct method to obtain such an a priori bound. In the process, we compare these theorems in terms of assumptions and outcomes.

In this paper we study impulsive periodic solutions for second-order nonautonomous singular differential equations. Our proof is based on the mountain pass theorem. Some recent results in the literature are extended.

This paper is devoted to the study of global existence of periodic solutions of a delayedtumor-immune competition model. Also some numerical simulations are given to illustratethe theoretical results

We consider the following model that describes the spread of n types of epidemics which are interdependent on each other:

Our aim is to establish criteria such that the above system has one or multiple constant-sign periodic solutions (u1, u2, …, un), that is, for each 1 ≤ i ≤ n, ui, is periodic and θiui ≥ 0 where θi, ε (1, −1) is fixed. Examples are also included to illustrate the results obtained.

A possible control strategy against the spread of an infectious disease is the treatmentwith antimicrobials that are given prophylactically to those that had contact with an infective person.The treatment continues until recovery or until it becomes obvious that there was no infectionin the first place. The model considers susceptible, treated uninfected exposed, treated infected,(untreated) infectious, and recovered individuals. The overly optimistic assumptions are made thattreated uninfected individuals are not susceptible and treated infected individuals are not infectious.Since treatment lengths are considered that have an arbitrary distribution, the model systemconsists of ordinary differential and integral equations. We study the impact of the treatment lengthdistribution on the large-time behavior of the model solutions, namely whether the solutions convergeto an equilibrium or whether they are driven into undamped oscillations.

We study the existence of spatial periodic solutions for nonlinearelliptic equations $- \Delta u \, + \, g(x,u(x)) = 0, \;x \in {\mathbb R}^N$ where g is a continuous function, nondecreasing w.r.t. u. Wegive necessary and sufficient conditions for the existence ofperiodic solutions. Some cases with nonincreasing functions gare investigated as well. As an application we analyze themathematical model of electron beam focusing system and we provethe existence of positive periodic solutions for the envelopeequation. We present also numerical simulations.

We develop the qualitative theory of thesolutions of the McKendrick partial differential equation ofpopulation dynamics. We calculate explicitly the weak solutionsof the McKendrick equation and of the Lotka renewal integralequation with time and age dependent birth rate. Mortality modulusis considered age dependent. We show the existence of demographycycles. For a population with only one reproductive age class,independently of the stability of the weak solutions and after atransient time, the temporal evolution of the number ofindividuals of a population is always modulated by a time periodicfunction. The periodicity of the cycles is equal to the age ofthe reproductive age class, and a population retains the memoryfrom the initial data through the amplitude of oscillations. For apopulation with a continuous distribution of reproductive ageclasses, the amplitude of oscillation is damped. The periodicityof the damped cycles is associated with the age of the firstreproductive age class. Damping increases as the dispersion of thefertility function around the age class with maximal fertilityincreases. In general, the period of the demography cycles isassociated with the time that a species takes to reach thereproductive maturity.

In this work, we introduce a new software created to study hematopoiesis at the cellpopulation level with the individually based approach. It can be used as an interface between theoreticalworks on population dynamics and experimental observations. We show that this softwarecan be useful to study some features of normal hematopoiesis as well as some blood diseases suchas myelogenous leukemia. It is also possible to simulate cell communication and the formation ofcell colonies in the bone marrow.

Let $1\leq p,q\leq\infty$, $s\in\mathbb{R}$ and let $X$ be a Banach space. We show that the analogue of Marcinkiewicz’s Fourier multiplier theorem on $L^p(\mathbb{T})$ holds for the Besov space $B_{p,q}^s(\mathbb{T};X)$ if and only if $1\ltp\lt\infty$ and $X$ is a UMD-space. Introducing stronger conditions we obtain a periodic Fourier multiplier theorem which is valid without restriction on the indices or the space (which is analogous to Amann’s result (Math. Nachr. 186 (1997), 5–56) on the real line). It is used to characterize maximal regularity of periodic Cauchy problems.

AMS 2000 Mathematics subject classification: Primary 47D06; 42A45

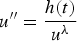
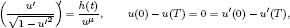
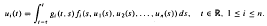
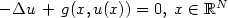
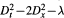We show that almost all perturbations P — λ, λ € C, of an arbitrary constant coefficient partial differential operator P are globally hypoelliptic on the torus. We also give a characterization of the values λ € C for which the operator is globally hypoelliptic; in particular, we show that the addition of a term of order zero may destroy the property of global hypoellipticity of operators of principal type, contrary to that happens with the usual (local) hypoellipticity.