Periodic solutions for indefinite singular perturbations of the relativistic acceleration
Published online by Cambridge University Press: 22 June 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Using the Leray–Schauder degree, we study the existence of solutions for the following periodic differential equation with relativistic acceleration and singular nonlinearity:
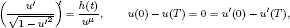
where μ > 1 and the weight h: [0, T] → ℝ is a continuous sign-changing function. There are no a priori estimates on the set of positive solutions (a condition used in general to apply the Leray–Schauder degree), and we prove that no solution of the equation appears on the boundary of an unbounded open set during the deformation to an autonomous problem.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 148 , Issue 4 , August 2018 , pp. 703 - 712
- Copyright
- Copyright © Royal Society of Edinburgh 2018
Footnotes
*
Present address: Departamento de Matemàticas, Universidad de Oviedo, Calle Federico García Lorca 18, 33007 Oviedo, Spain (mzamora@uniovi.es).
- 5
- Cited by

