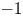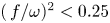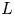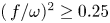Refine search
Actions for selected content:
107 results
Magneto-gravity-precessional instability
-
- Journal:
- Journal of Fluid Mechanics / Volume 1025 / 25 December 2025
- Published online by Cambridge University Press:
- 16 December 2025, A2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Frozen waves in the inertial regime
-
- Journal:
- Journal of Fluid Mechanics / Volume 1021 / 25 October 2025
- Published online by Cambridge University Press:
- 14 October 2025, A12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global instability of flows through single- and double-bifurcation airway models
-
- Journal:
- Journal of Fluid Mechanics / Volume 1020 / 10 October 2025
- Published online by Cambridge University Press:
- 06 October 2025, A32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Triad near-resonant instability of vertically bounded internal waves in non-uniform stratification
-
- Journal:
- Journal of Fluid Mechanics / Volume 1018 / 10 September 2025
- Published online by Cambridge University Press:
- 01 September 2025, A20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shape modes and jet formation on ultrasound-driven wall-attached bubbles
-
- Journal:
- Journal of Fluid Mechanics / Volume 1017 / 25 August 2025
- Published online by Cambridge University Press:
- 11 August 2025, A9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Enhancement of heat transfer using Faraday instability
-
- Journal:
- Journal of Fluid Mechanics / Volume 1016 / 10 August 2025
- Published online by Cambridge University Press:
- 04 August 2025, A35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A generalised multiparameter linear stability and sensitivity analysis method
-
- Journal:
- Journal of Fluid Mechanics / Volume 1011 / 25 May 2025
- Published online by Cambridge University Press:
- 15 May 2025, A12
-
- Article
- Export citation
Marangoni-driven patterns, ridges and hills in surfactant-covered parametric surface waves
-
- Journal:
- Journal of Fluid Mechanics / Volume 1008 / 10 April 2025
- Published online by Cambridge University Press:
- 10 April 2025, R4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Faraday waves and period tripling in a horizontal circular tank
-
- Journal:
- Journal of Fluid Mechanics / Volume 1006 / 10 March 2025
- Published online by Cambridge University Press:
- 03 March 2025, A4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wall-damped Faraday waves in horizontally oscillating two-layer fluid flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 1002 / 10 January 2025
- Published online by Cambridge University Press:
- 26 December 2024, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Atomisation of an acoustically levitated droplet: experimental observations of myriad complex phenomena
-
- Journal:
- Journal of Fluid Mechanics / Volume 999 / 25 November 2024
- Published online by Cambridge University Press:
- 21 November 2024, A89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Parametric oscillations of the sessile drop
-
- Journal:
- Journal of Fluid Mechanics / Volume 995 / 25 September 2024
- Published online by Cambridge University Press:
- 19 September 2024, A3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A revised gap-averaged Floquet analysis of Faraday waves in Hele-Shaw cells
-
- Journal:
- Journal of Fluid Mechanics / Volume 977 / 25 December 2023
- Published online by Cambridge University Press:
- 27 December 2023, A45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pattern evolution and modal decomposition of Faraday waves in a brimful cylinder
-
- Journal:
- Journal of Fluid Mechanics / Volume 974 / 10 November 2023
- Published online by Cambridge University Press:
- 10 November 2023, A56
-
- Article
- Export citation
Resonances and instabilities in a tilted rotating annulus
-
- Journal:
- Journal of Fluid Mechanics / Volume 973 / 25 October 2023
- Published online by Cambridge University Press:
- 20 October 2023, A34
-
- Article
- Export citation
The onset and saturation of the Faraday instability in miscible fluids in a rotating environment
-
- Journal:
- Journal of Fluid Mechanics / Volume 973 / 25 October 2023
- Published online by Cambridge University Press:
- 12 October 2023, A6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Superharmonic and triadic resonances in a horizontally oscillated stably stratified square cavity
-
- Journal:
- Journal of Fluid Mechanics / Volume 970 / 10 September 2023
- Published online by Cambridge University Press:
- 04 September 2023, A25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sliding, vibrating and swinging droplets on an oscillating fibre
-
- Journal:
- Journal of Fluid Mechanics / Volume 967 / 25 July 2023
- Published online by Cambridge University Press:
- 19 July 2023, A24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Parametric subharmonic instability of inertial shear at ocean fronts
-
- Journal:
- Journal of Fluid Mechanics / Volume 966 / 10 July 2023
- Published online by Cambridge University Press:
- 05 July 2023, A34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mechanics of removing water from the ear canal: Rayleigh–Taylor instability
-
- Journal:
- Journal of Fluid Mechanics / Volume 963 / 25 May 2023
- Published online by Cambridge University Press:
- 16 May 2023, A12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation