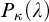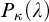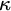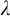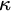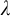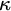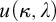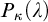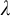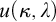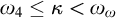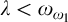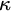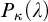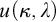The development of the forcing method has shown that several key questions regarding infinite sets cannot be settled under ZFC alone. The most widely supported view is that this undecidability simply reflects the limitations of ZFC in addressing all mathematical problems. This perspective has motivated an extensive search for new axioms—the so-called large cardinal axioms—which, when added to ZFC, yield a deeper and more robust understanding of the set-theoretic universe. Along this line, the dissertation is divided into three thematic blocks, each of them framed within these extensions of ZFC:

• • Very large cardinals at the threshold of Kunen inconsistency, with a focus on elementarity and cardinal correctness (Chapter 2).

• • Generalized Descriptive Set Theory at singular strong limit cardinals of countable cofinality, with a focus on two regularity properties (Chapter 3).

• • Covering lemmas and Woodin’s HOD Dichotomy through the lens of Shelah’s pcf theory (Chapter 4).

Specifically, Chapter 2 establishes an inconsistency result using tools from singular cardinal combinatorics and Shelah’s pcf theory, proving the nonexistence of cardinal preserving elementary embeddings into V and establishing thereby a limitation in the hierarchy of large cardinal axioms. The proof is based on the notion of good scales and its connection with Jónsson cardinals. Chapter 3 proves a consistency result obtained via a Prikry-type forcing construction, providing a singular-cardinal analogue of Solovay’s theorem. This thematic block is inspired by Woodin’s Axiom $I_0$ which provides the appropriate axiomatic framework to develop Generalized Descriptive Set Theory in generalized Baire/Cantor spaces at singular cardinals. Concretely, we construct a model of ZFC where $\kappa $ is a strong limit singular cardinal with countable cofinality, and every subset of ${}^\omega \kappa $ in $L(V_{\kappa +1})$ has both the $\kappa $-Perfect Set Property and the $\vec {\mathcal {U}}$-Baire Property. Chapter 4 further explores the study of “covering lemmas” and Woodin’s HOD Dichotomy, employing both the perspective and the tools of pcf theory. Specifically, the connection between the cover property and a new pcf-theoretic concept—called the scale property—is analyzed. This analysis builds a bridge between combinatorial principles in pcf theory and the structural behavior of HOD.

Abstract prepared by Sebastiano Thei.

E-mail: thei91.seba@gmail.com.

URL: https://air.uniud.it/handle/11390/1316344?mode=full.

Cummings, Foreman, and Magidor proved that Jensen’s square principle is non-compact at $\aleph _\omega $, meaning that it is consistent that $\square _{\aleph _n}$ holds for all $n<\omega $ while $\square _{\aleph _\omega }$ fails. We investigate the natural question of whether this phenomenon generalizes to singulars of uncountable cofinality. Surprisingly, we show that under some mild ${{\mathsf {PCF}}}$-theoretic hypotheses, the weak square principle $\square _\kappa ^*$ is in fact compact at singulars of uncountable cofinality.

We investigate pseudopowers of singular cardinals and deduce some consequences for covering numbers at singular cardinals of uncountable cofinality.

Let $\kappa $ be a regular uncountable cardinal, and a cardinal greater than or equal to $\kappa $. Revisiting a celebrated result of Shelah, we show that if is close to $\kappa $ and (= the least size of a cofinal subset of ) is greater than , then can be represented (in the sense of pcf theory) as a pseudopower. This can be used to obtain optimal results concerning the splitting problem. For example we show that if and , then no $\kappa $-complete ideal on is weakly -saturated.

We show that it is relatively consistent with ZFC to have PCF structures of height δ, for all ordinals δ < ω3.

We prove that a combinatorial consequence of the negation of the PCF conjecture for intervais, involving free subsets relative to set mappings, is not implied by even the strongest known large cardinal axiom.