Refine search
Actions for selected content:
3 results
A SCHWARZ LEMMA FOR
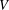 $V$ -HARMONIC MAPS AND THEIR APPLICATIONS
$V$ -HARMONIC MAPS AND THEIR APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 17 August 2017, pp. 504-512
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
SOME REMARKS ON THE PIGOLA–RIGOLI–SETTI VERSION OF THE OMORI–YAU MAXIMUM PRINCIPLE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 19 August 2013, pp. 337-342
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
ON MINIMAL SURFACES SATISFYING THE OMORI–YAU PRINCIPLE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 16 June 2011, pp. 33-39
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation