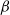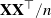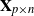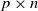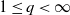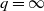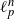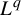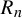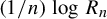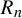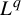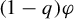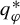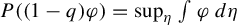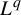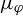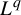134 results
Bankruptcy probabilities under non-poisson inspection
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 19 March 2025, pp. 1-40
-
- Article
- Export citation
16 - Hypothesis Testing: Error Exponents
- from Part III - Hypothesis Testing and Large Deviations
-
- Book:
- Information Theory
- Published online:
- 09 January 2025
- Print publication:
- 02 January 2025, pp 317-332
-
- Chapter
- Export citation
15 - Information Projection and Large Deviations
- from Part III - Hypothesis Testing and Large Deviations
-
- Book:
- Information Theory
- Published online:
- 09 January 2025
- Print publication:
- 02 January 2025, pp 296-316
-
- Chapter
- Export citation
Precise large deviations of the net loss process in a non-standard two-dimensional risk model
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 39 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 15 November 2024, pp. 44-63
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A sufficient condition for the quasipotential to be the rate function of the invariant measure of countable-state mean-field interacting particle systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 21 March 2024, pp. 960-1003
- Print publication:
- September 2024
-
- Article
- Export citation
Asymptotic results for sums and extremes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 13 March 2024, pp. 1153-1171
- Print publication:
- December 2024
-
- Article
- Export citation
Sharp large deviations and concentration inequalities for the number of descents in a random permutation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 810-833
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Differences between Lyapunov exponents for the simple random walk in Bernoulli potentials
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 23 June 2023, pp. 82-103
- Print publication:
- March 2024
-
- Article
- Export citation
Upper large deviations for power-weighted edge lengths in spatial random networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 June 2023, pp. 34-70
- Print publication:
- March 2024
-
- Article
- Export citation
Large deviations of extremal eigenvalues of sample covariance matrices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1275-1280
- Print publication:
- December 2023
-
- Article
- Export citation
Asymptotic persistence time formulae for multitype birth–death processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 21 March 2023, pp. 895-920
- Print publication:
- September 2023
-
- Article
- Export citation
1 - Introduction
-
- Book:
- Large Deviations for Markov Chains
- Published online:
- 03 August 2022
- Print publication:
- 27 October 2022, pp 1-13
-
- Chapter
- Export citation
8 - The Large Deviation Principle for Empirical Measures
-
- Book:
- Large Deviations for Markov Chains
- Published online:
- 03 August 2022
- Print publication:
- 27 October 2022, pp 117-133
-
- Chapter
- Export citation
11 - Large Deviations for Vector-Valued Additive Functionals
-
- Book:
- Large Deviations for Markov Chains
- Published online:
- 03 August 2022
- Print publication:
- 27 October 2022, pp 154-196
-
- Chapter
- Export citation

Large Deviations for Markov Chains
-
- Published online:
- 03 August 2022
- Print publication:
- 27 October 2022
Limit theorems for random points in a simplex
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 21 June 2022, pp. 685-701
- Print publication:
- September 2022
-
- Article
- Export citation
Return-time L^q -spectrum for equilibrium states with potentials of summable variation
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 06 June 2022, pp. 2489-2515
- Print publication:
- August 2023
-
- Article
- Export citation
7 - B-Graphs and the Continuity of the Limit limλ→0 ʋλ(s;q,r)
-
- Book:
- A Course in Stochastic Game Theory
- Published online:
- 05 May 2022
- Print publication:
- 26 May 2022, pp 94-110
-
- Chapter
- Export citation
Large-deviation results for triangular arrays of semiexponential random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 399-420
- Print publication:
- June 2022
-
- Article
- Export citation
Large-deviation asymptotics of condition numbers of random matrices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 1114-1130
- Print publication:
- December 2021
-
- Article
- Export citation