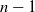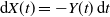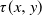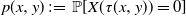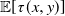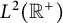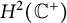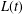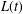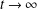Refine search
Actions for selected content:
107 results
3 - Law of Large Numbers and Central Limit Theorem
-
- Book:
- Probability Theory for Quantitative Scientists
- Published online:
- 24 July 2025
- Print publication:
- 14 August 2025, pp 43-90
-
- Chapter
- Export citation
Block–Savits type characterizations using the Laplace transform and some related issues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 22 April 2025, pp. 1193-1215
- Print publication:
- September 2025
-
- Article
- Export citation
Monotonic Weighted Power Transformations to Additivity
-
- Journal:
- Psychometrika / Volume 42 / Issue 1 / March 1977
- Published online by Cambridge University Press:
- 01 January 2025, pp. 83-109
-
- Article
- Export citation
On the Brownian range and the Brownian reversal
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 03 December 2024, pp. 775-794
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
2 - Review of Mathematics
-
- Book:
- Applied Hydrology
- Published online:
- 09 July 2024
- Print publication:
- 04 July 2024, pp 11-35
-
- Chapter
- Export citation
13 - The Laplace Transform
-
- Book:
- Signals, Systems, and Signal Processing
- Published online:
- 29 August 2024
- Print publication:
- 13 June 2024, pp 556-575
-
- Chapter
- Export citation
Oscillation-free point-to-point motions of planar differentially flat under-actuated robots: a Laplace transform method
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A first-passage-place problem for integrated diffusion processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 22 May 2023, pp. 55-67
- Print publication:
- March 2024
-
- Article
- Export citation
5 - Formal Models of Memory Based on Temporally-Varying Representations
-
-
- Book:
- New Handbook of Mathematical Psychology
- Published online:
- 20 April 2023
- Print publication:
- 27 April 2023, pp 218-264
-
- Chapter
- Export citation
On q-scale functions of spectrally negative Lévy processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 September 2022, pp. 56-84
- Print publication:
- March 2023
-
- Article
- Export citation
Appendix E - Fourier Series and Transforms
-
- Book:
- Liquid Crystals and their Computer Simulations
- Published online:
- 21 July 2022
- Print publication:
- 28 July 2022, pp 562-565
-
- Chapter
- Export citation
On Hardy kernels as reproducing kernels
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 17 June 2022, pp. 428-442
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Laplace transform approach to direct and inverse problems for multi-compartment models
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 16 March 2022, pp. 1170-1184
-
- Article
- Export citation
2 - The Basics of Feedback
-
- Book:
- A Guide to Feedback Theory
- Published online:
- 09 April 2021
- Print publication:
- 22 April 2021, pp 52-115
-
- Chapter
- Export citation
LAPLACE BOUNDS APPROXIMATION FOR AMERICAN OPTIONS
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 36 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 09 October 2020, pp. 514-547
-
- Article
- Export citation
LARGE DEVIATIONS FOR THE LONGEST GAP IN POISSON PROCESSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 16 October 2019, pp. 146-156
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
8 - Transient Dynamics
-
- Book:
- Theory and Computation in Hydrodynamic Stability
- Published online:
- 22 November 2018
- Print publication:
- 06 December 2018, pp 225-258
-
- Chapter
- Export citation
AGGREGATION OF DEPENDENT RISKS IN MIXTURES OF EXPONENTIAL DISTRIBUTIONS AND EXTENSIONS
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 48 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 25 April 2018, pp. 1079-1107
- Print publication:
- September 2018
-
- Article
- Export citation
Taylor's law, via ratios, for some distributions with infinite mean
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 15 September 2017, pp. 657-669
- Print publication:
- September 2017
-
- Article
- Export citation
Non-parametric estimation for a pure-jump Lévy process
-
- Journal:
- Annals of Actuarial Science / Volume 12 / Issue 2 / September 2018
- Published online by Cambridge University Press:
- 10 May 2017, pp. 338-349
-
- Article
- Export citation