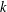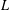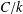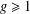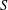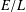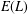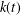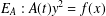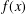Refine search
Actions for selected content:
2 results
1 - What Is the Mordell Conjecture (Faltings’s Theorem)?
-
- Book:
- The Mordell Conjecture
- Published online:
- 13 January 2022
- Print publication:
- 03 February 2022, pp 1-5
-
- Chapter
- Export citation
ON INTEGRAL POINTS ON ISOTRIVIAL ELLIPTIC CURVES OVER FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 27 March 2020, pp. 177-185
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation