No CrossRef data available.
Article contents
ON INTEGRAL POINTS ON ISOTRIVIAL ELLIPTIC CURVES OVER FUNCTION FIELDS
Published online by Cambridge University Press: 27 March 2020
Abstract
Let 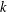 $k$ be a finite field and
$k$ be a finite field and 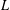 $L$ be the function field of a curve
$L$ be the function field of a curve 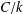 $C/k$ of genus
$C/k$ of genus 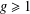 $g\geq 1$. In the first part of this note we show that the number of separable
$g\geq 1$. In the first part of this note we show that the number of separable 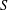 $S$-integral points on a constant elliptic curve
$S$-integral points on a constant elliptic curve 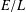 $E/L$ is bounded solely in terms of
$E/L$ is bounded solely in terms of 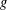 $g$ and the size of
$g$ and the size of 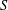 $S$. In the second part we assume that
$S$. In the second part we assume that 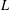 $L$ is the function field of a hyperelliptic curve
$L$ is the function field of a hyperelliptic curve 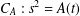 $C_{A}:s^{2}=A(t)$, where
$C_{A}:s^{2}=A(t)$, where 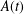 $A(t)$ is a square-free
$A(t)$ is a square-free 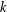 $k$-polynomial of odd degree. If
$k$-polynomial of odd degree. If  $\infty$ is the place of
$\infty$ is the place of 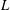 $L$ associated to the point at infinity of
$L$ associated to the point at infinity of 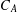 $C_{A}$, then we prove that the set of separable
$C_{A}$, then we prove that the set of separable 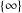 $\{\infty \}$-points can be bounded solely in terms of
$\{\infty \}$-points can be bounded solely in terms of 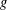 $g$ and does not depend on the Mordell–Weil group
$g$ and does not depend on the Mordell–Weil group 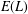 $E(L)$. This is done by bounding the number of separable integral points over
$E(L)$. This is done by bounding the number of separable integral points over 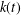 $k(t)$ on elliptic curves of the form
$k(t)$ on elliptic curves of the form 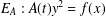 $E_{A}:A(t)y^{2}=f(x)$, where
$E_{A}:A(t)y^{2}=f(x)$, where 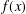 $f(x)$ is a polynomial over
$f(x)$ is a polynomial over 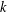 $k$. Additionally, we show that, under an extra condition on
$k$. Additionally, we show that, under an extra condition on 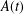 $A(t)$, the existence of a separable integral point of ‘small’ height on the elliptic curve
$A(t)$, the existence of a separable integral point of ‘small’ height on the elliptic curve 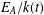 $E_{A}/k(t)$ determines the isomorphism class of the elliptic curve
$E_{A}/k(t)$ determines the isomorphism class of the elliptic curve 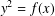 $y^{2}=f(x)$.
$y^{2}=f(x)$.
MSC classification
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 102 , Issue 2 , October 2020 , pp. 177 - 185
- Copyright
- © 2020 Australian Mathematical Publishing Association Inc.


