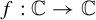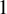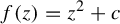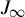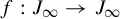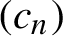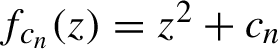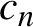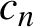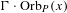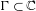Refine search
Actions for selected content:
7 results
On quasiconformal non-equivalence of gasket Julia sets and limit sets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 09 June 2025, pp. 3465-3489
- Print publication:
- November 2025
-
- Article
- Export citation
Lavaurs algorithm for cubic symmetric polynomials
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 06 January 2025, pp. 2314-2340
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transcendental Julia sets of minimal Hausdorff dimension
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 06 January 2025, pp. 2341-2413
- Print publication:
- August 2025
-
- Article
- Export citation
On invariant measures of ‘satellite’ infinitely renormalizable quadratic polynomials
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 13 November 2024, pp. 1843-1869
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Julia sets of Zorich maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 15 November 2021, pp. 692-728
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Total disconnectedness of Julia sets of random quadratic polynomials
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 04 March 2021, pp. 1764-1780
- Print publication:
- May 2022
-
- Article
- Export citation
Orbits of homogeneous polynomials on Banach spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 13 April 2020, pp. 1627-1655
- Print publication:
- June 2021
-
- Article
- Export citation