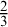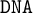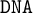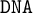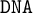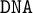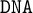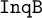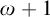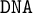Refine search
Actions for selected content:
5 results
STRICTLY n-FINITE VARIETIES OF HEYTING ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 29 October 2024, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Adding an implication to logics of perfect paradefinite algebras
-
- Journal:
- Mathematical Structures in Computer Science / Volume 34 / Issue 10 / November 2024
- Published online by Cambridge University Press:
- 02 October 2024, pp. 1138-1183
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DEGREE OF SATISFIABILITY IN HEYTING ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 09 January 2024, pp. 533-551
- Print publication:
- June 2025
-
- Article
- Export citation
THE AUTOMORPHISM GROUP OF THE FRAÏSSÉ LIMIT OF FINITE HEYTING ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 07 June 2022, pp. 1310-1320
- Print publication:
- September 2023
-
- Article
- Export citation
AN ALGEBRAIC APPROACH TO INQUISITIVE AND
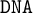 $\mathtt {DNA}$-LOGICS
$\mathtt {DNA}$-LOGICS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 02 December 2021, pp. 950-990
- Print publication:
- December 2022
-
- Article
- Export citation
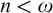
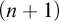
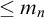
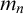
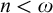
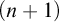
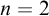
 ) order-preserving logics are non-algebraizable self-extensional logics of formal inconsistency and undeterminedness determined by a six-valued matrix. We studied these logics extensively in Gomes et al. ((2022).
) order-preserving logics are non-algebraizable self-extensional logics of formal inconsistency and undeterminedness determined by a six-valued matrix. We studied these logics extensively in Gomes et al. ((2022).  order-preserving and
order-preserving and