Refine search
Actions for selected content:
25 results
The geometric Satake equivalence for integral motives
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 17 December 2025, pp. 2755-2851
- Print publication:
- November 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SIMPLE TYPE THEORY FOR METAPLECTIC COVERS OF
 $\operatorname {GL}(r)$ OVER A NON-ARCHIMEDEAN LOCAL FIELD
$\operatorname {GL}(r)$ OVER A NON-ARCHIMEDEAN LOCAL FIELD
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 18 March 2025, pp. 1263-1335
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Kostant’s problem for parabolic Verma modules
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 27 January 2025, pp. 594-615
-
- Article
- Export citation
On the derived category of the Iwahori–Hecke algebra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 04 May 2023, pp. 1042-1110
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Gelfand–Graev representation of classical groups in terms of Hecke algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 24 June 2022, pp. 1343-1368
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Central elements in affine mod p Hecke algebras via perverse
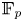 $\mathbb {F}_p$-sheaves
$\mathbb {F}_p$-sheaves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 14 September 2021, pp. 2215-2241
- Print publication:
- October 2021
-
- Article
- Export citation
Vanishing theorems for the mod p cohomology of some simple Shimura varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 03 November 2020, e38
-
- Article
-
- You have access
- Open access
- Export citation
THE
 $q$-SCHUR ALGEBRAS AND
$q$-SCHUR ALGEBRAS AND  $q$-SCHUR DUALITIES OF FINITE TYPE
$q$-SCHUR DUALITIES OF FINITE TYPE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 19 February 2020, pp. 129-160
- Print publication:
- January 2022
-
- Article
- Export citation
Springer correspondence for the split symmetric pair in type
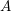 $A$
$A$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 11 / November 2018
- Published online by Cambridge University Press:
- 11 October 2018, pp. 2403-2425
- Print publication:
- November 2018
-
- Article
- Export citation
ONE-DIMENSIONAL STOCHASTIC MODELS WITH OPEN BOUNDARIES: INTEGRABILITY, APPLICATIONS AND
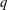 $q$-DEFORMED KNIZHNIK–ZAMOLODCHIKOV EQUATIONS
$q$-DEFORMED KNIZHNIK–ZAMOLODCHIKOV EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 19 August 2015, pp. 520-521
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
GEOMETRIC TAMELY RAMIFIED LOCAL THETA CORRESPONDENCE IN THE FRAMEWORK OF THE GEOMETRIC LANGLANDS PROGRAM
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 3 / July 2016
- Published online by Cambridge University Press:
- 18 February 2015, pp. 625-671
- Print publication:
- July 2016
-
- Article
- Export citation
Level 1 Hecke algebras of modular forms modulo
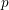 $p$
$p$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 3 / March 2015
- Published online by Cambridge University Press:
- 27 November 2014, pp. 397-415
- Print publication:
- March 2015
-
- Article
- Export citation
The centralizer of a subgroup in a group algebra
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 20 November 2012, pp. 49-56
-
- Article
-
- You have access
- Export citation
AN EIGENSPACE OF LARGE DIMENSION FOR A HECKE ALGEBRA ON AN
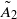 BUILDING
BUILDING
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 28 September 2011, pp. 29-54
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
A Satake isomorphism in characteristic p
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 23 August 2010, pp. 263-283
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
Leading coefficients and cellular bases of Hecke algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 653-677
-
- Article
-
- You have access
- Export citation
On Ihara’s lemma for Hilbert modular varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 5 / September 2009
- Published online by Cambridge University Press:
- 09 September 2009, pp. 1114-1146
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Nearly ordinary rank four Galois representations and $p$-adic Siegel modular forms
-
- Journal:
- Compositio Mathematica / Volume 142 / Issue 5 / September 2006
- Published online by Cambridge University Press:
- 25 September 2006, pp. 1122-1156
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
Hecke algebras of classical type and their representation type
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 91 / Issue 2 / September 2005
- Published online by Cambridge University Press:
- 23 August 2005, pp. 355-413
- Print publication:
- September 2005
-
- Article
- Export citation
Quantum Weyl reciprocity for cohomology
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 90 / Issue 3 / May 2005
- Published online by Cambridge University Press:
- 22 April 2005, pp. 655-688
- Print publication:
- May 2005
-
- Article
- Export citation


























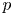
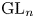
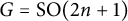
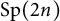
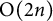
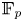
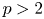
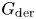
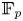
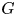
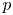
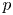
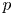
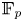
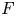




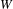
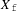
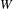


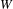


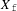


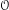
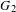
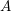
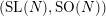


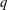

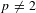
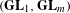

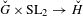
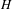
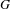
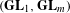
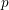
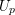
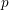
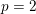
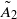 BUILDING
BUILDING
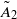 and let 𝔸 be its fundamental apartment. We consider the set 𝕌
and let 𝔸 be its fundamental apartment. We consider the set 𝕌