Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mantero, A. M.
and
Zappa, A.
2013.
A representation of the chamber set Hecke algebra of an affine building.
Ricerche di Matematica,
Vol. 62,
Issue. 2,
p.
341.
Mantero, A. M.
and
Zappa, A.
2014.
Eigenspaces of operator algebras on the fundamental apartment of an affine building.
Ricerche di Matematica,
Vol. 63,
Issue. 2,
p.
273.

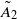 BUILDING
BUILDING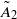 and let 𝔸 be its fundamental apartment. We consider the set 𝕌
and let 𝔸 be its fundamental apartment. We consider the set 𝕌