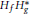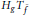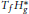Refine search
Actions for selected content:
5 results
On spectra of Hankel operators on the polydisc
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 301-317
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
5 - State Equivalence, State Reduction
- from Part I - Lectures on Basics with Examples
-
- Book:
- Time-Variant and Quasi-separable Systems
- Published online:
- 24 October 2024
- Print publication:
- 31 October 2024, pp 73-86
-
- Chapter
- Export citation
Characterizations of Hankel operators in the essential commutant of quasicontinuous Toeplitz operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 09 February 2021, pp. 44-51
- Print publication:
- March 2022
-
- Article
- Export citation
Bounded Hankel Products on the Bergman Space of the Polydisk
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 1 / 01 February 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 190-204
- Print publication:
- 01 February 2009
-
- Article
-
- You have access
- Export citation
ADMISSIBLE AND WEAKLY ADMISSIBLE OBSERVATION OPERATORS FOR THE RIGHT SHIFT SEMIGROUP
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 45 / Issue 2 / June 2002
- Published online by Cambridge University Press:
- 17 June 2002, pp. 353-362
-
- Article
-
- You have access
- Export citation