No CrossRef data available.
Article contents
Bounded Hankel Products on the Bergman Space of the Polydisk
Part of:
Special classes of linear operators
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We consider the problem of determining for which square integrable functions 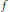 $f$ and
$f$ and  $g$ on the polydisk the densely defined Hankel product
$g$ on the polydisk the densely defined Hankel product 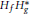 ${{H}_{f}}\,H_{g}^{*}$ is bounded on the Bergman space of the polydisk. Furthermore, we obtain similar results for the mixed Haplitz products
${{H}_{f}}\,H_{g}^{*}$ is bounded on the Bergman space of the polydisk. Furthermore, we obtain similar results for the mixed Haplitz products 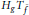 ${{H}_{g}}\,{{T}_{{\bar{f}}}}$ and
${{H}_{g}}\,{{T}_{{\bar{f}}}}$ and 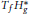 ${{T}_{f}}\,H_{g}^{*}$ , where
${{T}_{f}}\,H_{g}^{*}$ , where 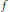 $f$ and
$f$ and  $g$ are square integrable on the polydisk and
$g$ are square integrable on the polydisk and 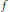 $f$ is analytic.
$f$ is analytic.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2009
References
[2]
Stroethoff, K. and Zheng, D., Products of Hankel and Toeplitz operators on the Bergman space. J. Funct. Anal. 169 (1999), no. 1, 289–313.Google Scholar
[3]
Stroethoff, K. and Zheng, D., Bounded Toeplitz products on the Bergman space of the polydisk. J. Math. Anal. Appl. 278 (2003), no. 1, 125–135.Google Scholar
[4]
Stroethoff, K. and Zheng, D., Algebraic and spectral properties of dual Toeplitz operators. Trans. Amer. Math. Soc. 354 (2002), no. 6, 2495–2520.Google Scholar
[5]
Stroethoff, K. and Zheng, D., Toeplitz and Hankel operators on Bergman spaces. Trans. Amer. Math. Soc. 329 (1992), no. 2, 773–794.Google Scholar
[6]
Lu, Y., Commuting dual Toeplitz operators with pluriharmonic symbols. J. Math. Anal. Appl. 302 (2005), no. 1, 149–156.Google Scholar
[7]
Zhu, K. H., Operator theory in function spaces.
Monographs and Textbooks in Pure and Applied Mathematics 139, Marcel Dekker, New York, 1990.Google Scholar
- 5
- Cited by

