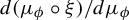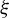We prove a result on equilibrium measures for potentials with summable variation on arbitrary subshifts over a countable amenable group. For finite configurations v and w, if v is always replaceable by w, we obtain a bound on the measure of v depending on the measure of w and a cocycle induced by the potential. We then use this result to show that under this replaceability condition, we can obtain bounds on the Lebesgue–Radon–Nikodym derivative 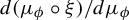$d (\mu _\phi \circ \xi ) / d\mu _\phi $ for certain holonomies 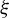$\xi $ that generate the homoclinic (Gibbs) relation. As corollaries, we obtain extensions of results by Meyerovitch [Gibbs and equilibrium measures for some families of subshifts. Ergod. Th. & Dynam. Sys. 33(3) (2013), 934–953], and García-Ramos and Pavlov [Extender sets and measures of maximal entropy for subshifts. J. Lond. Math. Soc. (2) 100(3) (2019), 1013–1033] to the countable amenable group subshift setting. Our methods rely on the exact tiling result for countable amenable groups by Downarowicz, Huczek, and Zhang [Tilings of amenable groups. J. Reine Angew. Math. 2019(747) (2019), 277–298] and an adapted proof technique from García-Ramos and Pavlov.

Fully Bayesian estimation of item response theory models with logistic link functions suffers from low computational efficiency due to posterior density functions that do not have known forms. To improve algorithmic computational efficiency, this paper proposes a Bayesian estimation method by adopting a new data-augmentation strategy in uni- and multidimensional IRT models. The strategy is based on the Pólya–Gamma family of distributions which provides a closed-form posterior distribution for logistic-based models. In this paper, an overview of Pólya–Gamma distributions is described within a logistic regression framework. In addition, we provide details about deriving conditional distributions of IRT, incorporating Pólya–Gamma distributions into the conditional distributions for Bayesian samplers’ construction, and random drawing from the samplers such that a faster convergence can be achieved. Simulation studies and applications to real datasets were conducted to demonstrate the efficiency and utility of the proposed method.

History of the development of the reciprocal lattice is reviewed. The reciprocal lattice as an essential tool for the study of diffraction experiments by ordered structures and characterization of their structural properties is widely taught in any text of solid state or chemistry, but usually without discussion of its history. This article aims to give a coherent historical perspective on the reciprocal lattice. First, a basic introduction to the reciprocal lattice concept, its mathematical foundation and physical origin, and its relationship with the direct lattice is provided. Then a detailed chronicle of ideas leading to the concept of the reciprocal lattice is presented, including a review of the contributions of Gibbs, Ewald, and others. The polar lattice concept, the great ancestor of the reciprocal lattice, is presented.