Refine search
Actions for selected content:
18 results
A characterization of virtually free groups among hyperbolic groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 13 January 2025, pp. 477-483
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
2 - Transformation and Tensors
-
- Book:
- An Introduction to Gravity
- Published online:
- 04 May 2024
- Print publication:
- 11 April 2024, pp 51-101
-
- Chapter
- Export citation
3 - Geodesics
-
- Book:
- Einstein's General Theory of Relativity
- Published online:
- 15 June 2023
- Print publication:
- 29 June 2023, pp 44-84
-
- Chapter
- Export citation

Einstein's General Theory of Relativity
- A Concise Introduction
-
- Published online:
- 15 June 2023
- Print publication:
- 29 June 2023
4 - Lifting Geometry to Mapping Spaces II: (Weak) Riemannian Metrics
-
- Book:
- An Introduction to Infinite-Dimensional Differential Geometry
- Published online:
- 08 December 2022
- Print publication:
- 22 December 2022, pp 80-105
-
- Chapter
-
- You have access
- Open access
- Export citation
5 - Riemannian Geometry
-
- Book:
- Mathematical Methods for Physics
- Published online:
- 08 December 2022
- Print publication:
- 22 December 2022, pp 170-232
-
- Chapter
- Export citation
RETRACTED - THE KRONECKER–WEYL EQUIDISTRIBUTION THEOREM AND GEODESICS IN 3-MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 21 March 2022, pp. 1-44
-
- Article
- Export citation
An Overview of General Relativity
-
- Book:
- A Student's Guide to Special Relativity
- Published online:
- 26 January 2022
- Print publication:
- 03 February 2022, pp 145-176
-
- Chapter
- Export citation
Special curves in modular surfaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 December 2021, pp. 1-18
- Print publication:
- March 2023
-
- Article
- Export citation
Open problems and questions about geodesics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 06 December 2019, pp. 641-684
- Print publication:
- March 2021
-
- Article
- Export citation
1 - Geometry of Surfaces in R3
-
- Book:
- A Comprehensive Introduction to Sub-Riemannian Geometry
- Published online:
- 28 October 2019
- Print publication:
- 31 October 2019, pp 11-44
-
- Chapter
- Export citation
The Sea Mile and Nautical Mile in Marine Navigation
-
- Journal:
- The Journal of Navigation / Volume 72 / Issue 3 / May 2019
- Published online by Cambridge University Press:
- 21 December 2018, pp. 805-812
- Print publication:
- May 2019
-
- Article
- Export citation
ON THE EXISTENCE OF FINITE CRITICAL TRAJECTORIES IN A FAMILY OF QUADRATIC DIFFERENTIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 80-91
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
A Short Note on Short Pants
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 4 / 01 December 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 870-876
- Print publication:
- 01 December 2014
-
- Article
-
- You have access
- Export citation
Subriemannian geodesics of Carnot groups of step 3∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 19 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 12 June 2012, pp. 274-287
- Print publication:
- January 2013
-
- Article
- Export citation
The structure of reachable sets for affine control systemsinduced by generalized Martinet sub-Lorentzian metrics
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 16 January 2012, pp. 1150-1177
- Print publication:
- October 2012
-
- Article
- Export citation
Bergman metrics and geodesics in the space of Kähler metrics on principally polarized abelian varieties
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 21 June 2011, pp. 1-25
- Print publication:
- January 2012
-
- Article
- Export citation
A NOTE ON THE UNCLOUDING THE SKY OF NEGATIVELY CURVED MANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 413-424
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
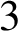
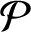
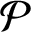

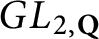

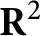
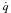
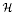 of smooth Kähler metrics in a fixed Kähler class on a polarized Kähler manifold is well approximated by finite-dimensional submanifolds
of smooth Kähler metrics in a fixed Kähler class on a polarized Kähler manifold is well approximated by finite-dimensional submanifolds 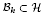 of Bergman metrics of height
of Bergman metrics of height 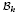 . For any polarized Kähler manifold, the approximation is in the
. For any polarized Kähler manifold, the approximation is in the 