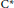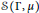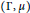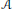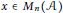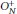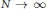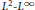Refine search
Actions for selected content:
7 results
Generalized Meixner-type free gamma distributions: Convolution formulas and potential correspondence
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 17 November 2025, pp. 1-37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectra of infinite graphs via freeness with amalgamation
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 03 October 2022, pp. 1633-1684
- Print publication:
- October 2023
-
- Article
- Export citation
Matrix Liberation Process II: Relation to Orbital Free Entropy
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 28 January 2020, pp. 493-541
- Print publication:
- April 2021
-
- Article
- Export citation
Freeness and The Partial Transposes of Wishart Random Matrices
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 659-681
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Free Product C*-algebras Associated with Graphs, Free Differentials, and Laws of Loops
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 3 / 01 June 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 548-578
- Print publication:
- 01 June 2017
-
- Article
-
- You have access
- Export citation
On Two-faced Families of Non-commutative Random Variables
-
- Journal:
- Canadian Journal of Mathematics / Volume 67 / Issue 6 / 01 December 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1290-1325
- Print publication:
- 01 December 2015
-
- Article
-
- You have access
- Export citation
Strong Asymptotic Freeness for Free Orthogonal Quantum Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 4 / 01 December 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 708-720
- Print publication:
- 01 December 2014
-
- Article
-
- You have access
- Export citation