We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let X1, X2, · ·· be a sequence of independent, identically distributed (i.i.d.) random variables with positive mean. An analogue of Rényi's (1962) stochastic geyser problem is solved for the associated process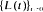 
of first-passage times. More precisely, it is shown that a single realization of the sequence 
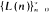determines the distribution function (d.f.) of the Xn's almost surely (a.s.), even if the observations are erroneous up to an order o(log n).
