Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Edrington, T.
1970.
Setting Threshold Levels According to Mean First-Passage Time.
IEEE Transactions on Aerospace and Electronic Systems,
Vol. AES-6,
Issue. 3,
p.
410.
Lixin, Zhang
1996.
Necessary conditions for renewal processes approximating to Wiener processes.
Applied Mathematics,
Vol. 11,
Issue. 4,
p.
459.

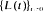 of first-passage times. More precisely, it is shown that a single realization of the sequence
of first-passage times. More precisely, it is shown that a single realization of the sequence 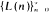 determines the distribution function (d.f.) of the
determines the distribution function (d.f.) of the 