Refine search
Actions for selected content:
16 results
14 - Stochastic Differential Equations
- from Part III - Pricing by Dynamic Replication
-
- Book:
- Derivatives Pricing
- Published online:
- 08 July 2025
- Print publication:
- 20 March 2025, pp 309-327
-
- Chapter
- Export citation
Representing Sudden Shifts in Intensive Dyadic Interaction Data Using Differential Equation Models with Regime Switching
-
- Journal:
- Psychometrika / Volume 83 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 01 January 2025, pp. 476-510
-
- Article
- Export citation
Fitting Nonlinear Ordinary Differential Equation Models with Random Effects and Unknown Initial Conditions Using the Stochastic Approximation Expectation–Maximization (SAEM) Algorithm
-
- Journal:
- Psychometrika / Volume 81 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 01 January 2025, pp. 102-134
-
- Article
- Export citation

Higher Special Functions
- A Theory of the Central Two-Point Connection Problem Based on a Singularity Approach
-
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024
A new lifetime distribution by maximizing entropy: properties and applications
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 28 February 2023, pp. 189-206
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the oscillation of certain second-order linear differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 09 December 2022, pp. 1965-1992
- Print publication:
- December 2023
-
- Article
- Export citation
Appendix E - Separation of Variables
-
- Book:
- Quantum Mechanics
- Published online:
- 11 February 2023
- Print publication:
- 15 September 2022, pp 547-548
-
- Chapter
- Export citation
On non-separated zero sequences of solutions of a linear differential equation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 247-261
-
- Article
- Export citation
Solution of some Engineering Partial Differential Equations Governed by the Minimal of a Functional by Global Optimization Method
-
- Journal:
- Journal of Mechanics / Volume 29 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 01 May 2013, pp. 507-516
- Print publication:
- September 2013
-
- Article
- Export citation
On the complex oscillation for a class of homogeneous linear differential equations
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 43 / Issue 1 / February 2000
- Published online by Cambridge University Press:
- 20 January 2009, pp. 1-13
-
- Article
-
- You have access
- Export citation
THREE NONNEGATIVE SOLUTIONS FOR SECOND-ORDER IMPULSIVE DIFFERENTIAL EQUATIONS WITH A THREE-POINT BOUNDARY VALUE PROBLEM
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 3 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 337-346
-
- Article
-
- You have access
- Export citation
On the collapsibility of lifetime regression models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 755-772
- Print publication:
- September 2003
-
- Article
- Export citation
First passage times of a jump diffusion process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 22 February 2016, pp. 504-531
- Print publication:
- June 2003
-
- Article
- Export citation
A note on level-crossing analysis for the excess, age, and spread distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 39 / Issue 4 / December 2002
- Published online by Cambridge University Press:
- 14 July 2016, pp. 896-900
- Print publication:
- December 2002
-
- Article
- Export citation
On the virtual waiting time in an M/G/1 retrial queue
-
- Journal:
- Journal of Applied Probability / Volume 28 / Issue 2 / June 1991
- Published online by Cambridge University Press:
- 14 July 2016, pp. 446-460
- Print publication:
- June 1991
-
- Article
- Export citation
The moments of the random variable for the number of returns of a simple random walk
-
- Journal:
- Advances in Applied Probability / Volume 19 / Issue 2 / June 1987
- Published online by Cambridge University Press:
- 01 July 2016, pp. 505-507
- Print publication:
- June 1987
-
- Article
-
- You have access
- Export citation
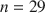
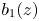
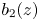
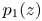
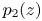
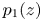
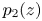
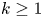
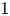
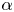
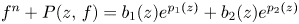
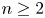
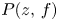
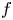
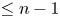
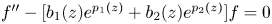
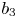
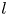
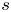
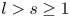
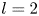
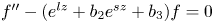
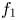
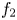
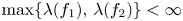
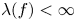
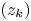
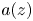
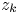
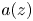
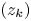
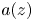
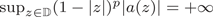
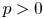
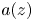
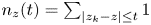
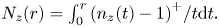
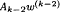 + … +
+ … + 