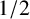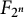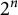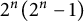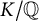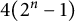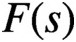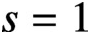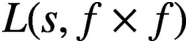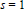Refine search
Actions for selected content:
6 results
ON THE LOWEST ZERO OF THE DEDEKIND ZETA FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 22 October 2024, pp. 460-468
- Print publication:
- June 2025
-
- Article
- Export citation
EXPLICIT MERTENS’ THEOREMS FOR NUMBER FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 169-172
- Print publication:
- August 2023
-
- Article
-
- You have access
- HTML
- Export citation
Arithmetically equivalent fields in a Galois extension with Frobenius Galois group of 2-power degree
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 13 June 2022, pp. 380-394
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LARGE VALUES OF L-FUNCTIONS ON THE 1-LINE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 02 October 2020, pp. 230-243
- Print publication:
- April 2021
-
- Article
- Export citation
1 - The Riemann zeta function
-
- Book:
- Zeta and L-Functions of Varieties and Motives
- Published online:
- 28 April 2020
- Print publication:
- 07 May 2020, pp 6-19
-
- Chapter
- Export citation
Upper Bounds on |L(1, χ)| and Applications
-
- Journal:
- Canadian Journal of Mathematics / Volume 50 / Issue 4 / 01 August 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 794-815
- Print publication:
- 01 August 1998
-
- Article
-
- You have access
- Export citation