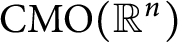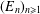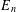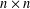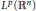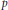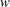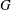Refine search
Actions for selected content:
21 results
Lorentz boundedness and compactness of Riesz transform commutator on stratified Lie groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 15 September 2025, pp. 1-28
-
- Article
- Export citation
9 - Excursion: Quantum Mechanics in a Nutshell
-
- Book:
- Advanced Linear Algebra
- Published online:
- 27 May 2025
- Print publication:
- 12 June 2025, pp 252-271
-
- Chapter
- Export citation
FINITE LINEAR COMBINATIONS OF MONOMIAL TOEPLITZ PRODUCTS ON THE BERGMAN SPACE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 39-60
- Print publication:
- August 2025
-
- Article
- Export citation
Products of commutators in matrix rings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 14 January 2025, pp. 512-529
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Powers of commutators in linear algebraic groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 14 May 2024, pp. 830-837
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
3 - Observables and Operators
-
- Book:
- Quantum Mechanics in Nanoscience and Engineering
- Published online:
- 11 May 2023
- Print publication:
- 01 June 2023, pp 10-15
-
- Chapter
- Export citation
A revisit on the compactness of commutators
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 20 August 2020, pp. 1667-1697
- Print publication:
- December 2021
-
- Article
- Export citation
5 - Nilpotent Groups, Commutators and Nilprogressions
-
- Book:
- Introduction to Approximate Groups
- Published online:
- 31 October 2019
- Print publication:
- 14 November 2019, pp 81-108
-
- Chapter
- Export citation
ORTHOMODULAR-VALUED MODELS FOR QUANTUM SET THEORY
-
- Journal:
- The Review of Symbolic Logic / Volume 10 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 05 June 2017, pp. 782-807
- Print publication:
- December 2017
-
- Article
- Export citation
THE DIMENSION OF CENTRALISERS OF MATRICES OF ORDER
 $n$
$n$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 26 September 2016, pp. 353-361
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
On the Commutators of Singular Integral Operators with Rough Convolution Kernels
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 4 / 01 August 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 816-840
- Print publication:
- 01 August 2016
-
- Article
-
- You have access
- Export citation
Compact Commutators of Rough Singular Integral Operators
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 1 / 01 March 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 19-29
- Print publication:
- 01 March 2015
-
- Article
-
- You have access
- Export citation
WORDS AND PRONILPOTENT SUBGROUPS IN PROFINITE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 29 September 2014, pp. 343-364
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Marcinkiewicz Commutators with Lipschitz Functions in Non-homogeneous Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 3 / 01 September 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 646-662
- Print publication:
- 01 September 2012
-
- Article
-
- You have access
- Export citation
From Matrix to Operator Inequalities
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 2 / 01 June 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 339-350
- Print publication:
- 01 June 2012
-
- Article
-
- You have access
- Export citation
STATES ON THE CUNTZ ALGEBRAS AND p-ADIC RANDOM WALKS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 19 July 2011, pp. 197-211
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
ENDPOINT ESTIMATES FOR COMMUTATORS OF RIESZ TRANSFORMS ASSOCIATED WITH SCHRÖDINGER OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 16 August 2010, pp. 367-389
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Bol Loops of Nilpotence Class Two
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 2 / 01 April 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 296-310
- Print publication:
- 01 April 2007
-
- Article
-
- You have access
- Export citation
The higher order commutators of the fractional integrals on Hardy spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 1 / August 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 11-24
- Print publication:
- August 2005
-
- Article
-
- You have access
- Export citation
A Generalized Characterization of Commutators of Parabolic Singular Integrals
-
- Journal:
- Canadian Mathematical Bulletin / Volume 42 / Issue 4 / 01 December 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 463-477
- Print publication:
- 01 December 1999
-
- Article
-
- You have access
- Export citation