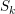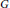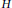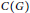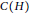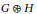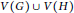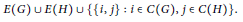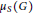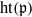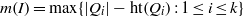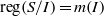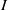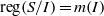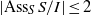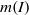Refine search
Actions for selected content:
7 results
ON THE ASYMPTOTIC BEHAVIOR OF THE VASCONCELOS INVARIANT FOR GRADED MODULES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 258 / June 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 296-310
- Print publication:
- June 2025
-
- Article
- Export citation
F-THRESHOLDS OF GRADED RINGS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 229 / March 2018
- Published online by Cambridge University Press:
- 07 December 2016, pp. 141-168
- Print publication:
- March 2018
-
- Article
-
- You have access
- HTML
- Export citation
Cover Product and Betti Polynomial of Graphs
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 2 / 01 June 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 320-333
- Print publication:
- 01 June 2015
-
- Article
-
- You have access
- Export citation
ON A CLASS OF MONOMIAL IDEALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 28 January 2013, pp. 514-526
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
ON THE REGULARITY CONJECTURE FOR THE COHOMOLOGY OF FINITE GROUPS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 51 / Issue 2 / June 2008
- Published online by Cambridge University Press:
- 28 July 2008, pp. 273-284
-
- Article
-
- You have access
- Export citation
Syzygies, multigraded regularity and toric varieties
-
- Journal:
- Compositio Mathematica / Volume 142 / Issue 6 / November 2006
- Published online by Cambridge University Press:
- 24 November 2006, pp. 1499-1506
- Print publication:
- November 2006
-
- Article
-
- You have access
- Export citation
Linear free resolutions over non-commutative algebras
-
- Journal:
- Compositio Mathematica / Volume 140 / Issue 4 / July 2004
- Published online by Cambridge University Press:
- 04 December 2007, pp. 1053-1058
- Print publication:
- July 2004
-
- Article
-
- You have access
- Export citation