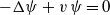Refine search
Actions for selected content:
3 results
On Calderon's problem for the connection Laplacian
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 05 January 2024, pp. 1087-1112
- Print publication:
- June 2025
-
- Article
- Export citation
SEMILINEAR CALDERÓN PROBLEM ON STEIN MANIFOLDS WITH KÄHLER METRIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 20 May 2020, pp. 132-144
- Print publication:
- February 2021
-
- Article
- Export citation
New global stability estimates for the Calderón problem in two dimensions
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 07 June 2012, pp. 553-569
- Print publication:
- July 2013
-
- Article
- Export citation